물리학에서 첫 번째로 다루는 가장 기초적인 학습 내용은 운동학(kinematics)으로 변화하는 세계의 움직이는 물체를 표현하고, 이 물체가 앞으로 어떻게 움직일 지를 예측하는 데 매우 큰 도움이 된다. 운동을 이해하기 위해 우리는 운동의 원인에 관계없이 먼저 시간과 공간의 개념을 활용해 운동을 기술하는 법을 익힐 것이다.
Kinematics is a branch of classical mechanics that describes the motion of points, bodies,
and systems of bodies(groups of objects) without considering the forces.
Edmund Taylor Whittaker (1904). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies
- 운동학은 동역학의 하위 분야로 운동 기하학으로도 불린다. (Russell C. Hibbeler (2009). Kinematics and kinetics of a particle)
고전역학의 세부분야
① 운동학(kinematics): 물체의 운동을 기술하는 고전역학의 세부분야
- 운동학에서 물체란, 입자 또는 다수의 입자가 모여 이루어진 물체-계(objects-system)를 의미한다.
② 동역학(dynamics): 물체의 운동을 야기하는 힘의 요소를 다루는 고전역학의 세부분야로, 때에 따라 운동학의 상위 분야로 포함되기도 한다.
- 동역학은 물체의 종류에 따라 다시 강체동역학, 연체동역학, 유체동역학으로 분류된다.
입자모형(particle model): 고전역학에서 입자 모형은 이상적인 물체 운동을 기술하기 위한 핵심 가정으로 '점입자(point particle)'를 가정한다. 점입자는 수학에서의 점(dot)과 같이 더 이상의 물리적 변형을 가할 수 없는 것으로, 물리학에서 point particle은 질량만 존재할 뿐 크기(size)나 부피(volume)가 존재하지 않는다.
위치, 속력, 그리고 속도
입자의 위치(position) x는 좌표계 상에서 원점이라 가정한 기준점에 대한 정량적 좌표값을 의미한다.
- 시간에 따른 입자의 공간 위치를 알면 입자의 운동을 기술할 수 있다.
변위(displacement)

■
- 정의: 변위란, 입자위치의 양적 변화량으로 나중 위치 값에서 처음 위치 값을 뺀 '벡터량'이다.
① 변위의 값이 양이면 운동 방향은 양의 방향을 나타낸다.
② 변위의 값이 음이면 운동 방향은 음의 방향을 나타낸다.
③ 운동 방향은 일반적으로 오른쪽을 양의 방향으로, 왼쪽을 음의 방향으로 잡는다.
- 단위: [m] 미터
- 물리량
① 델타 Δ는 변화량을 표시하는 기호로, 물리량 앞에 델타 기호는 그 물리량의 종류와 상관없이 '최종 값'에서 '초기 값'을 빼라는 의미를 갖는다.
② x_f: 입자의 최종(final) 위치
③ x_i: 입자의 초기(initial) 위치

그림 1. 변위와 이동거리의 차이
변위의 특징
1. 변위는 물체의 운동 변화량(크기)과 함께 방향을 반드시 고려해야 하는 벡터량이다.
2. 벡터량으로서 변위의 부호는 일반적으로 다음과 같이 정의한다.
1) 오른쪽으로 움직이는 물체는 Δx>0이다. 즉, 양수 부호를 갖는다.
2) 왼쪽으로 움직이는 물체는 Δx<0이다. 즉, 음수 부호를 갖는다.

그림 2. 물체의 운동방향과 변위의 부호
이동거리(distance travelled, 기호: d): 이동방향과 상관없이 입자가 이동한 총 경로의 길이를 의미한다.
- 이동거리는 크기만 갖는 스칼라량이다.
- 입자가 이동한 총 이동거리로 값의 크기는 변위보다 크거나 또는 같다.

평균속도와 평균속력
평균속도(average velocity)

■
- 정의: 변위를 변위가 발생한 시간 간격으로 나눈 값
- 단위: [m/s] 미터 퍼 세컨드
- 평균속도는 벡터량이다.
평균속도의 특징
1. 일반적으로 입자가 오른쪽으로 움직이면 평균속도는 양의 값을 갖는다.
- x가 양수이면서 크기가 증가하고 있거나, x가 음수이면서 절댓값이 줄어들고 있을 때 입자는 +x축(+x-)으로 운동하고, v_x, avg는 양수이다.
2. 같은 논리로, 입자가 왼쪽으로 움직이면 평균속도는 음의 값을 갖는다.
- x가 음수이면서 크기가 감소하고 있거나, 음수이면서 절댓값이 늘고 있을 때 입자는 -x-으로 운동하고, v_x, avg는 음수이다.
3. 위치-시간 그래프(s-t 그래프)에서 평균속도는 높이 Δx이고, 밑변 Δt인 직각삼각형의 빗변(직선기울기, slope의 비)으로 표현된다.

그림 3. 위치-시간 그래프(graph of position versus time)에서 평균속도는 직선기울기로 나타난다.
평균속력(average speed)
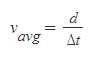
■
- 정의: 전체 이동거리(d_travel)를 이동하는 데 총 걸린 시간으로 나눈 값
- 단위: [m/s]
- 평균속력은 평균속도의 스칼라량이다.
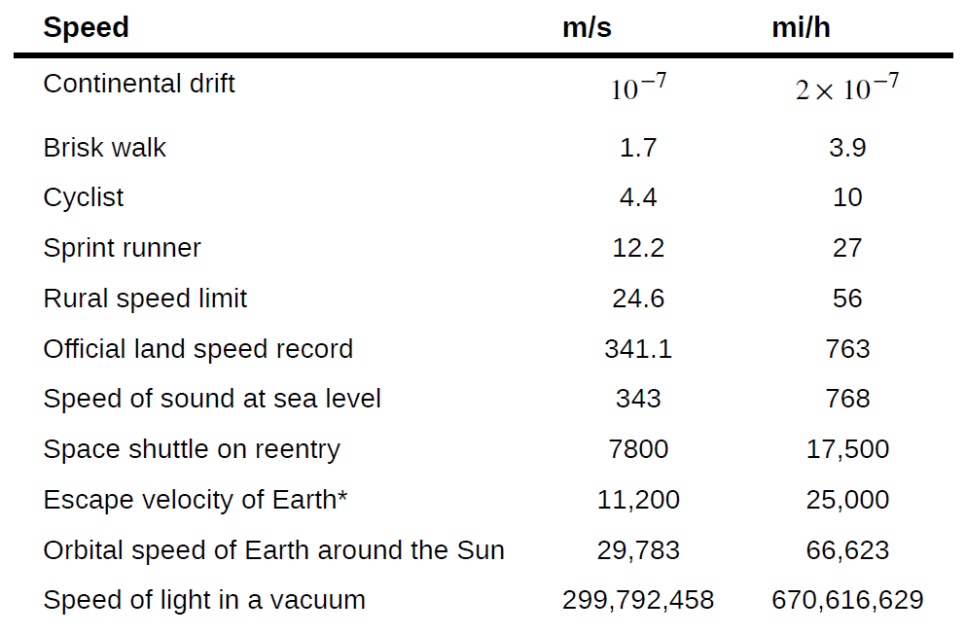
표 1. 물체의 평균적인 속력값 테이블
순간속도과 순간속력
순간속도 v_x는 시간 간격이 0으로 한없이 접근(근접, approach to Δt→0)할 때 평균속도의 극한 값이다.
순간속도
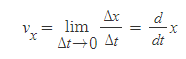
■
물리학에서 속도란 일반적으로 '순간속도'를 의미한다.
순간속력
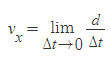
■
일정한 속도에서의 운동
일정한 속도는 간단히 등속(constant velocity)운동이라 하며, 등속 운동을 하는 입자의 최종 위치식은 다음과 같다.
PROOF. 등속운동을 하는 입자의 최종위치
$\left[1\right]\ 등속운동을\ 하는\ 물체의\ 속도는\ 평균속도이다.$[1] 등속운동을 하는 물체의 속도는 평균속도이다.
$\left[2\right]\ v_x=v_{x,\ avg}=\frac{\left(x_f-x_i\right)}{\Delta t}\ \Leftrightarrow \ v_x\Delta t=x_f-x_i$[2] vx=vx, avg=(xf−xi)Δt ⇔ vxΔt=xf−xi
$\left[3\right]\ x_f=x_i+v_x\Delta t$[3] xf=xi+vxΔt
$\left[4\right]\ \Delta t=t_f-t_i에서\ 처음\ 위치에\ 놓인\ 물체에\ 주어진\ 시간은\ t_i=0으로\ 둔다.$[4] Δt=tf−ti에서 처음 위치에 놓인 물체에 주어진 시간은 ti=0으로 둔다.

□
등속운동을 하는 입자의 최종위치
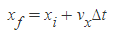
■
입자의 속도가 일정하면, 시간 내의 어떤 순간에서의 순간 속도는 이 구간에서의 평균속도와 같다.
'고급물리학' 카테고리의 다른 글
| 힘의 특징 (0) | 2021.11.06 |
|---|---|
| 힘의 개념과 장 (0) | 2021.11.06 |
| 뉴턴 이전 초기 고전역학 (0) | 2021.11.06 |
| 길이, 시간, 그리고 질량 (0) | 2021.11.06 |
| 물리학 지식의 특징 (0) | 2021.11.06 |