위치벡터, 속도벡터, 그리고 가속도 벡터
위치벡터: 위치벡터함수(position vector function)로 표현되는 벡터, 원점 O에서 점 P에 이른다.
속도벡터: 속도벡터함수(velocity vector function) 또는 접선벡터함수(tangential vector function)으로 표현되는 벡터, 위치벡터의 각 성분별 시간 미분
가속도 벡터: 가속도벡터함수(acceleration vector function)로 표현되는 벡터, 속도벡터의 시간 미분
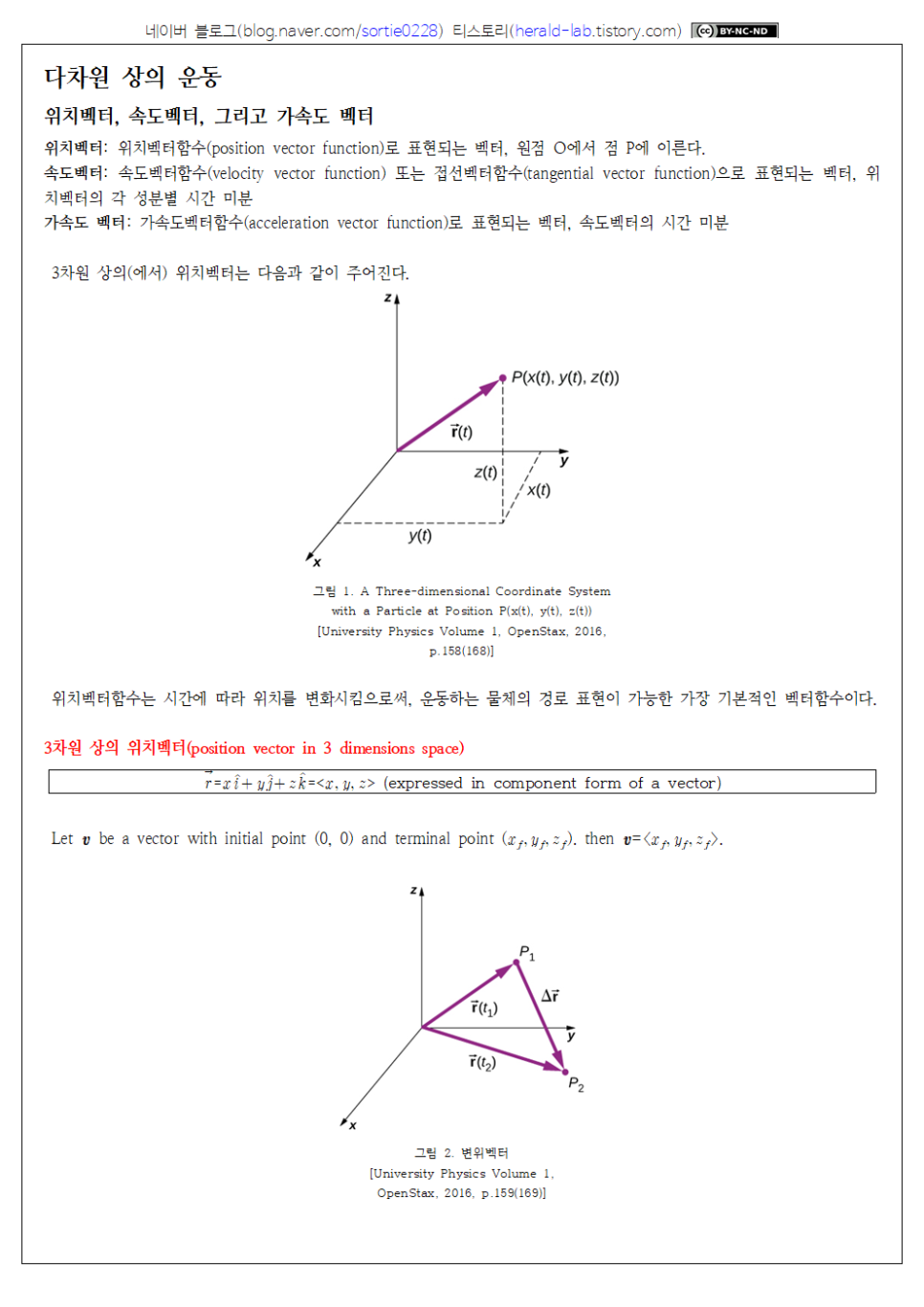
3차원 상의(에서) 위치벡터는 다음과 같이 주어진다.
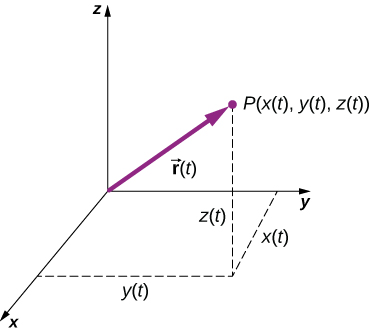
위치벡터함수는 시간에 따라 위치를 변화시킴으로써, 운동하는 물체의 경로 표현이 가능한 가장 기본적인 벡터함수이다.

Let v be a vector with initial point (0, 0) and terminal point (x_f, y_f, z_f). then =<x_f, y_f, z_f>.
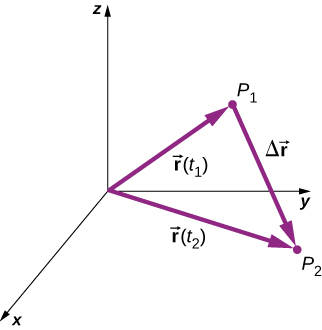
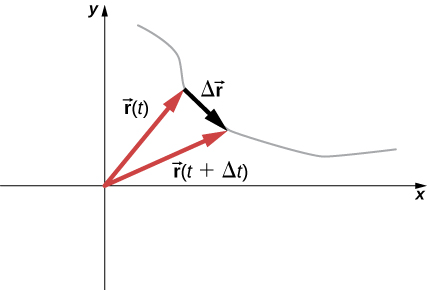
변위벡터는 특정시간 동안 움직이는 임자의 ‘나중 위치벡터’에서 ‘처음 위치벡터’를 뺀 값이다.
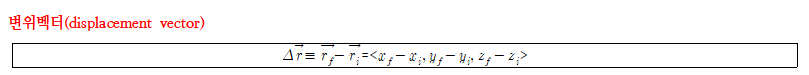
- 의미: 위치벡터의 변화량
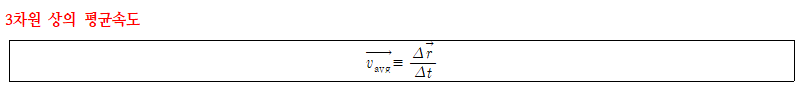
- 정의: 입자의 변위를 시간간격으로 나눈 값
- 방향: 변위벡터의 방향과 일치한다.
- 두 점 사이의 평균속도는 입자가 택한 경로와 무관하다.
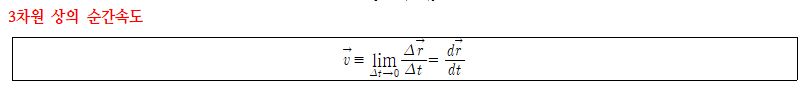
- 정의: 시간에 대한 위치벡터의 도함수, 또는 위치벡터의 각 성분별 시간 미분(시간에 대한 미분한 값)
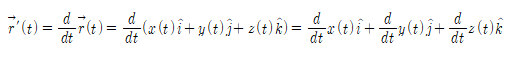
- 방향: 입자의 경로 상에 있는 임의의 점에서, 순간 속도벡터의 방향은 그 점에서의 경로접선과 일치하고 입자의 운동방향과 같다.
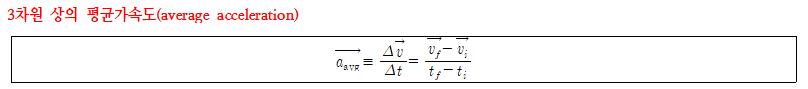
- 정의: 평균가속도는 순간 속도의 벡터의 변화를 걸린 시간으로 나눈 비와 같다.
- 방향: 평균가속도의 방향은 와 같다.
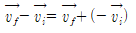
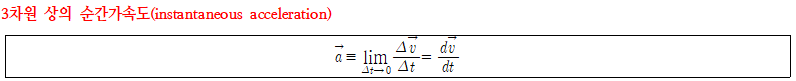
- 정의: 시간에 대한 속도벡터의 일차 도함수, 시간에 대한 위치벡터의 이차 도함수
일반적으로 속도 벡터는 순간속도 벡터를 가속도 벡터는 순간가속도 벡터를 의미한다.
일정한 가속도를 가지고 있는 이차원 상의 물체의 운동
2차원의 운동은 x-와 y-방향의 각각 독립된 운동으로 기술할 수 있다.
- 각 축의 방향은 서로 독립되게 존재한다. ⇒ y-의 운동에 변화를 주는 요인이 x-의 운동에 영향을 주지 않는다.
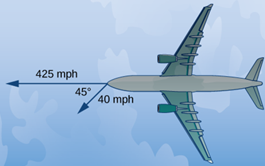
e.g. [그림 4]와 같이 축 방향으로 초기속도를 가지는 비행기에 축 방향으로 바람이 불어온다고 가정하자. 이때, 물체의 속도는 여전히 이다. 왜냐하면 각각의 방향에 대한 운동은 서로 독립되기 때문이다. 단, 물체의 방향으로 라는 속도가 추가된다.
2차원의 평면상에서 운동하는 입자의 위치벡터의 미분 결과는 아래와 같이 계산된다.
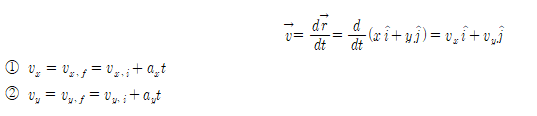


자유낙하운동

이탈리아의 천문학자 갈릴레이(Galileo Galilei, 1564~1642)는 자신이 고안한 실험을 통해 공기의 저항이 없는 조건에서, 지표면 부근의 모든 물체는 질량과 관계없이 동등한 중력가속도를 가진다고 생각했다. ⇒ 지구의 중력에 의해 물체는 일정한 높이에서 중력가속도라는 등가속도를 가지며, 중력가속도(등가속도)의 방향은 항상 지구중심부를 향한다.
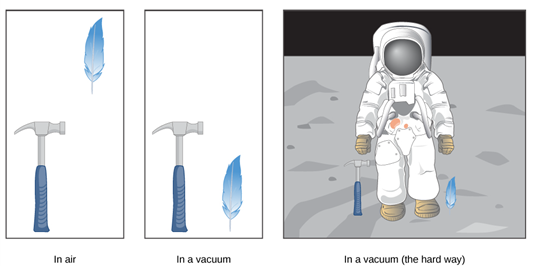

자유낙하(freely falling): 공기저항이 부재한 조건에서, 지표면으로 떨어지는 물체의 가속도운동
- 1971년 8월 2일, 미국의 공학자인 데이비드 스콧(David Scott, 1932~; NASA group 3 사령관(미공군 대령))의 달에서의(during the Moon landing) 자유낙하실험 ⇒ 달에서 동전과 종잇조각을 동시에 떨어뜨린 결과, 둘은 달의 표면에 동시에 떨어졌다.
- 자유낙하가속도(중력가속도): vector g로 표현하며, 크기는 |g|, 지표면을 기준으로 방향은 지구 중심부를 향한다.
· 중력가속도는 고도가 높아짐에 따라 감소한다.
· 중력가속도는 질량분포에 기인하기 때문에, 위도에 따라서도 크기가 약간씩 달라진다. ⇒ 지구의 실제 모양은 완전한 구체가 아닌 타원이고, 적도가 극지방보다 좀 더 두툼하다.
중력 가속도의 크기는 9.8[m/s^2]으로 근사한다.
자유낙하물체: 처음의 운동 상태와는 무관하게 중력만의 영향 하에 자유롭게 움직이는 물체로 아래와 같은 조건에서 물체는 자유낙하 한다.
1. 연직하방물체: (위에서)아래로 떨어뜨리는 물체
2. 연직상방물체: (아래에서)위로 던진 물체
3. 포물체

cf. 단, 는 자유낙하가속도의 크기를 나타내므로 양의 부호를 갖는다.
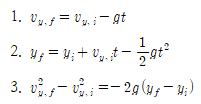
■
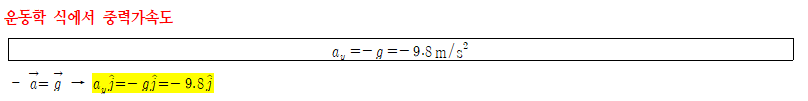
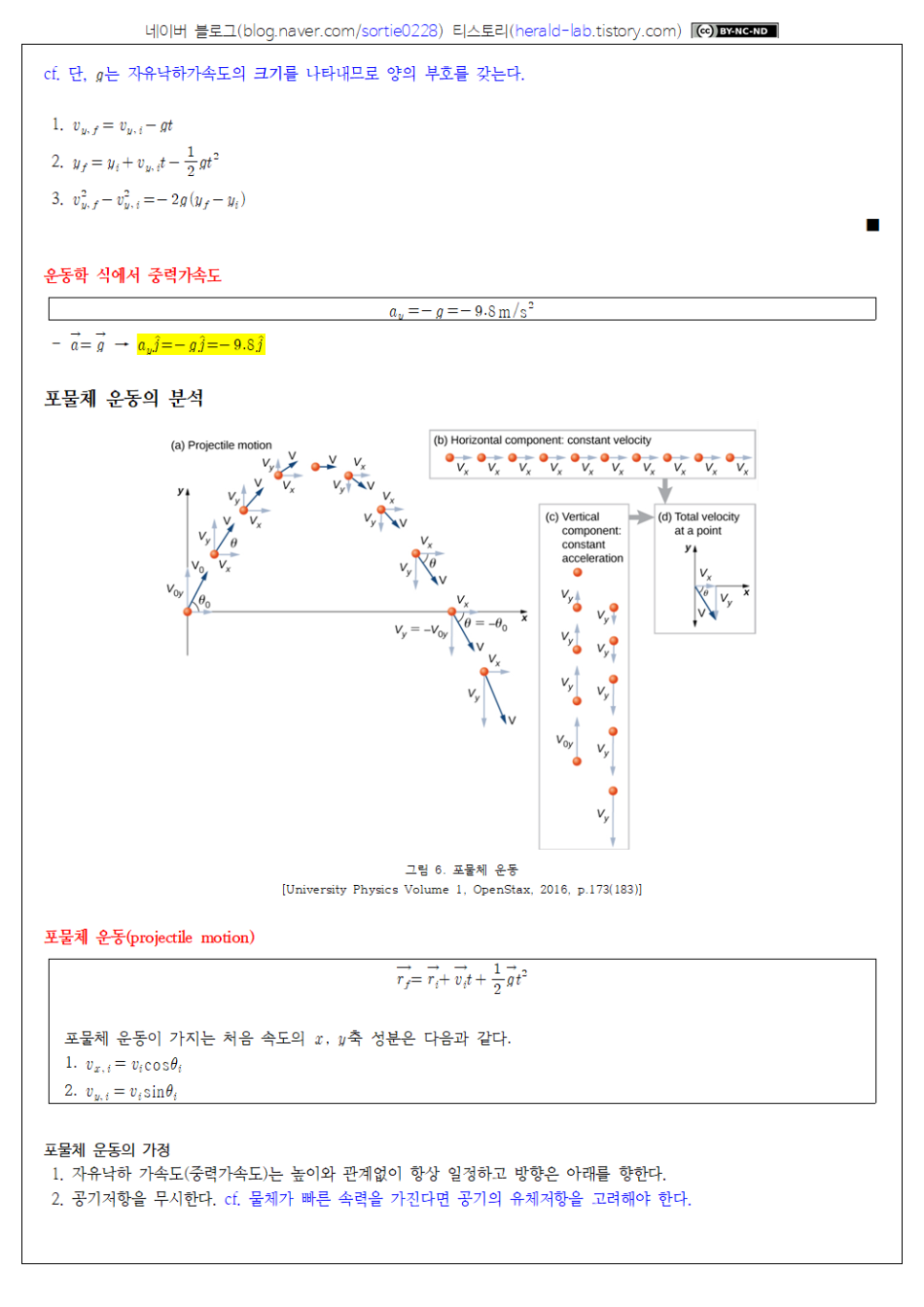
포물체 운동의 분석
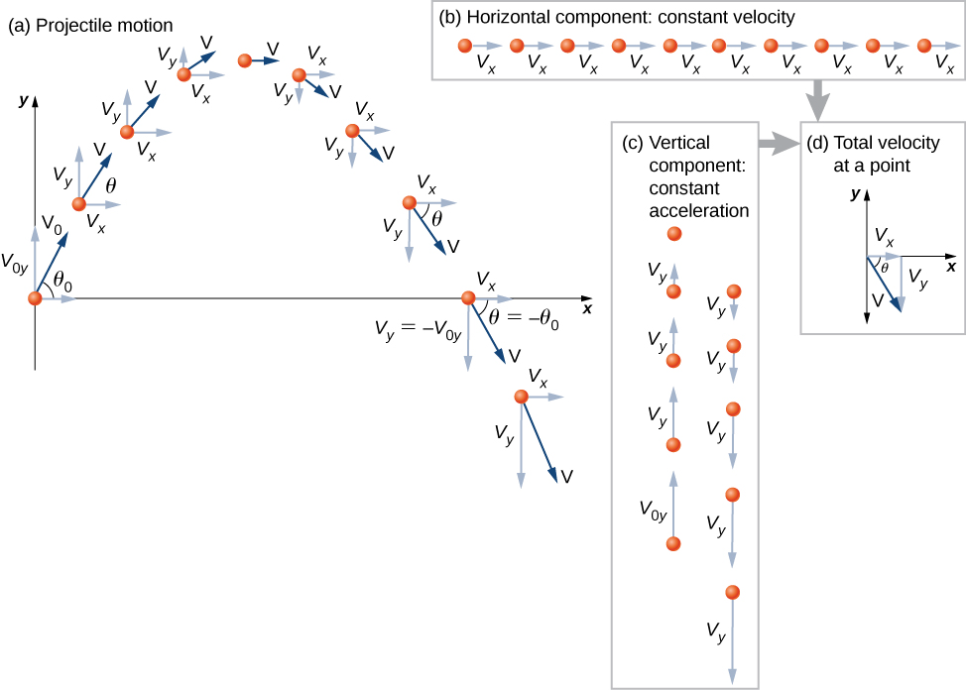

포물체 운동의 가정
1. 자유낙하 가속도(중력가속도)는 높이와 관계없이 항상 일정하고 방향은 아래를 향한다.
2. 공기저항을 무시한다. cf. 물체가 빠른 속력을 가진다면 공기의 유체저항을 고려해야 한다.
포물체 운동의 분석

포물체 운동의 분석: 포물체의 최대수평도달거리와 최대 연직 높이
t_i=0일 때, 포물체를 +v_y, i 성분 방향으로 쏘아 올리는 상황을 떠올려 보자.
- 포물체는 최고점(v_y, (max)=0)을 지나 포물체를 처음 쏘아올린 수평면 높이로 되돌아온다.
포물체운동의 분석에서 특별히 관심을 두는 위치는 다음과 같다.
① 최고점: 포물체가 가지는 최대 연직방향위치(y-) ⇒ 최고점의 xy좌표(x, y): (R/2, h)
② 최종점: 포물체가 가지는 최대 수평방향위치(x-) ⇒ 최종점의 xy좌표(x, y): (R, v_y, f=0)
포물체 운동에서의 물리량과 그 특징
1. 수평도달거리: 포물체가 수평방향으로 나가간 최대거리로 그 크기를 R로 표현한다.
2. 최대높이: 포물체가 연직방향으로 올라간 최대높이로 최고점에서는 v_y, (max)=0을 만족한다. 따라서 아래와 같은 식을 세울 수 있다.

3. 최대높이 도달시(time at which the projectile reaches peaks): 포물체가 최대높이에 도달하는 데 걸린 시간으로 최대높이의 수식 조건으로부터 쉽게 유도할 수 있다.
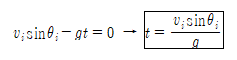
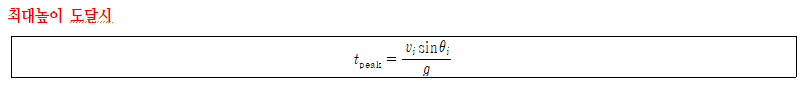
PROOF. 최대 높이
최대높이 도달시를 대입해 최대높이를 계산할 수 있다.

■
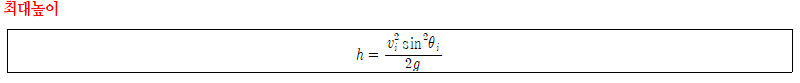
PROOF. 수평도달거리
[1] 포물체가 수평도달거리에 도달하기 위해선 최대높이 도달시의 2배가 되는 시간이 필요하다.
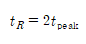
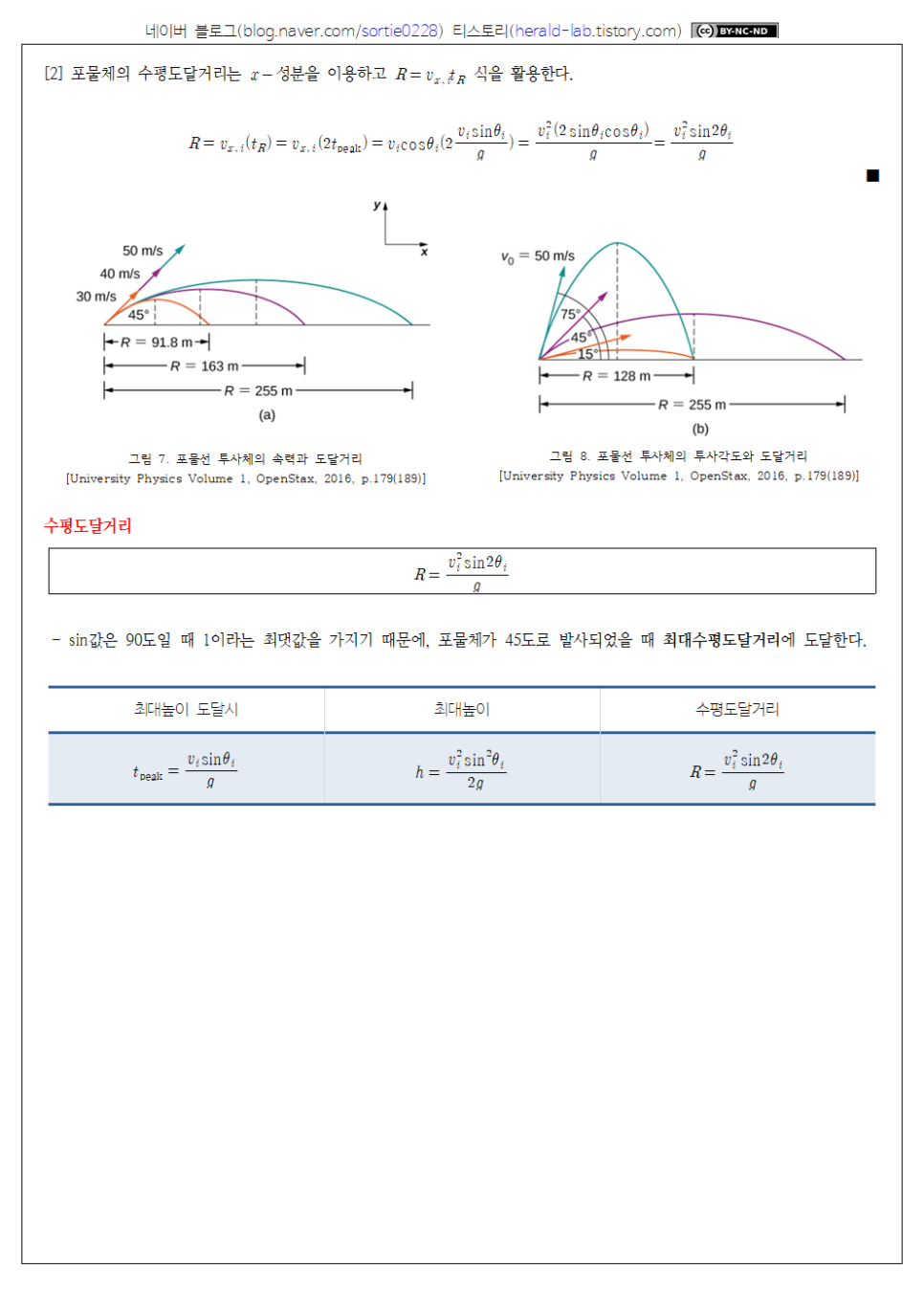
[2] 포물체의 수평도달거리는 성분을 이용하고 식을 활용한다.
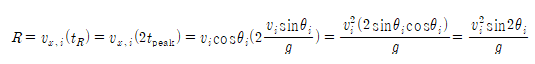
■
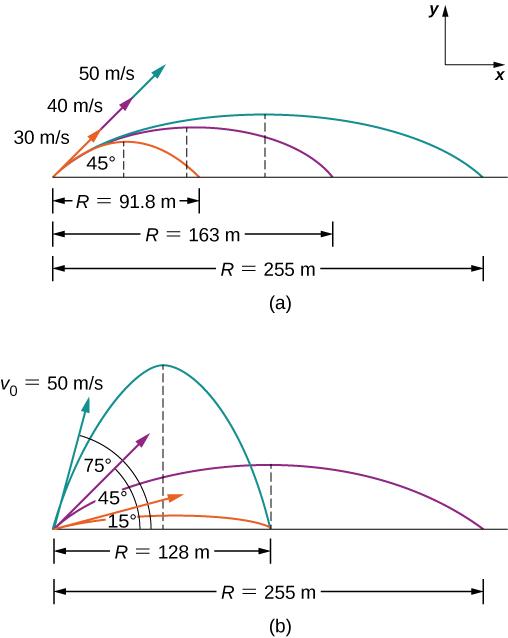
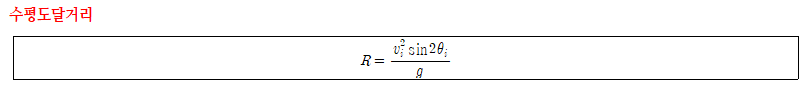
- sin값은 90도일 때 1이라는 최댓값을 가지기 때문에, 포물체가 45도로 발사되었을 때 최대수평도달거리에 도달한다.





'고급물리학' 카테고리의 다른 글
| 가우스의 법칙 (0) | 2021.12.05 |
|---|---|
| 열역학 학습을 위한 열화학 기초 (0) | 2021.12.02 |
| 지진파 Seismic Wave – 지진파의 이해 (0) | 2021.11.26 |
| 신경세포와 근육세포 (0) | 2021.11.21 |
| 귀의 소리증폭 - 물리학적 접근 (0) | 2021.11.21 |