전기 선속 Electric Flux
전기 선속(전기다발, electric flux): 전기장에 수직한 방향으로 놓인 단면적을 통과하는 전기력선의 묶음
- 단위 넓이 당 전기력선의 수는 전기장의 크기에 비례한다.
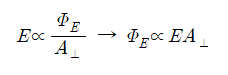
- 의미: 전기 선속은 어떤 면을 통과하는 전기력선의 수에 비례한다.
- 단위: [Nm^2/C]
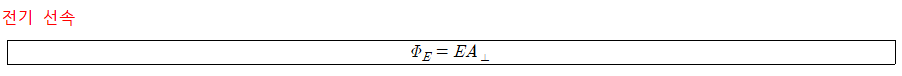
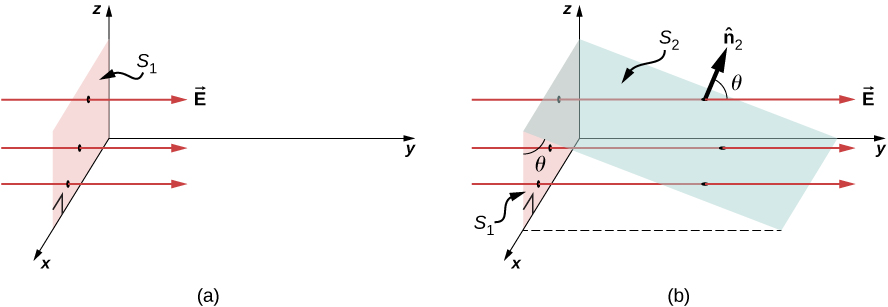
전기장의 방향과 표면적이 수직하지 않는 경우(φ)는,
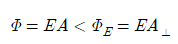
한 대소 관계를 따르며, 전기장에 수직한 표면적과 그렇지 않은 표면적 사이에는 다음과 같은 관계식이 존재한다.


전기 선속의 크기
전기 선속의 크기는 아래와 같이 정리할 수 있다.
1. 면에 대한 법선이 전기장의 방향과 평행일 때 전기 선속의 크기는 최댓값을 갖는다.
2. 면에 대한 법선이 전기장의 방향과 수직일 때 전기 선속의 크기는 0이다. ⇒ 알짜 전기선속이 0이다.
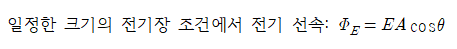
전기장이 균일하지 않은 경우, 전기장은 넓은 면에 걸쳐 변할 수 있으므로, 주어진 선속에 대한 앞선 정의는 미소 넓이 요소에 한정된다.

전기장과 표면적의 법선벡터는 모두 벡터량이고 코사인 항이 또한 존재하므로 둘을 스칼라곱으로 표현할 수 있다.
표면을 통과하는 전체 선속의 근삿값은 모든 요소에 대한 선속을 합하여 얻을 수 있고, 만약 각 요소의 넓이를 0에 근접하게 만든다면, 요소의 수는 무한히 많아지며 그 합은 적분으로 대신 표현할 수 있다.
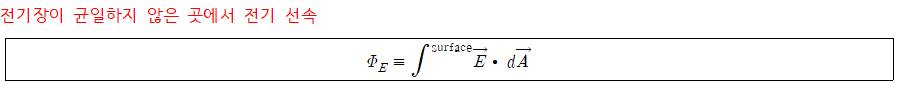
- 의미: 선속의 값은 전기장의 형태와 표면에 의해 결정된다.
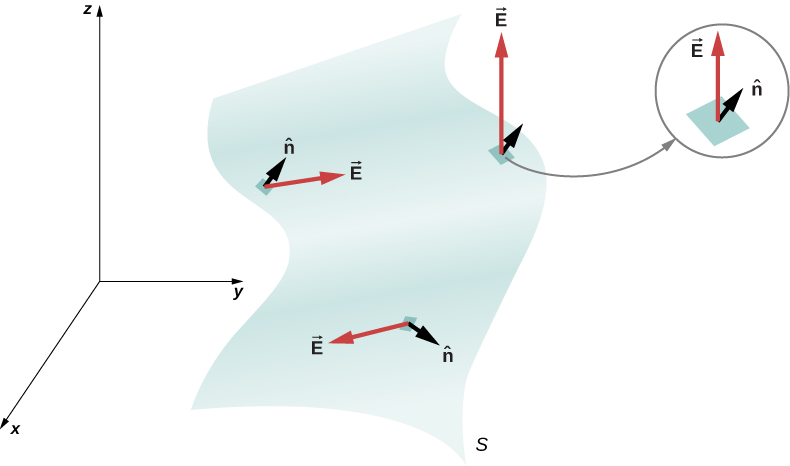
닫힌곡면에서의 선속
닫힌곡면(가우스 면, 가우스 곡면, closed surface, Gauss's surface): 내부공간과 외부공간을 완벽히 분리하고, 이 면을 지나지 않고서는 한 공간에서 다른 공간으로 이동할 수 없는 표면
알짜 전기력선 수란, 표면을 통과하여 나가는 전기력선 수에 표면을 통과하여 들어오는 전기력선 수를 뺀 값이다.
- 양의 선속: 나가는 전기력선 수 들어오는 전기력선 수
- 음의 선속: 나가는 전기력선 수 들어오는 전기력선 수
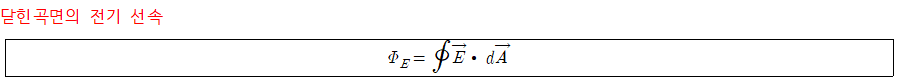
- 물리량
·∮: 적분하려는 면이 닫혀있음(닫힌곡면)을 의미한다.
- 의미: 전기장의 크기를 계산할 시, 표면에 수직한 전기장 성분만을 고려한다.

가우스 법칙
가우스 곡면을 지나는 알짜 전기 선속과 닫힌곡면 내의 양전하 사이의 관계를 알아보자.

- 물리량
· r: 전하와 가우스면 사이의 거리
· q: 가우스 면에 갇힌 전하
어떤 가우스 구면의 위치든 전기장의 크기는 같다. 전기장의 방향은 구면 바깥쪽을 향한다.

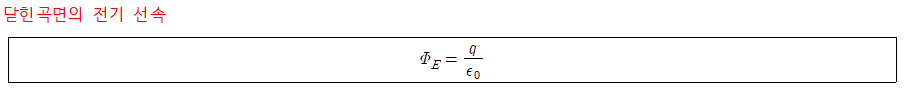
- 의미: 구면을 통과하는 알짜 선속은 구면 내부에 존재하는 전하량에 비례한다.

점전하 를 둘러싼 닫힌곡면을 지나는 알짜 선속은 가우스 곡면의 모양과는 무관하고, 크기는 항상 으로 주어진다.

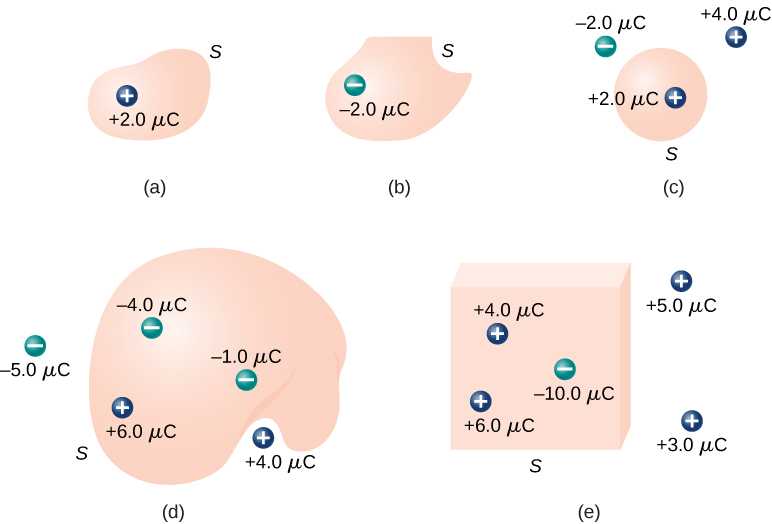
독일의 수학자이자 천문학자인 가우스(Carl Friedrich Gauss, 1777~1855)가 정리한 식으로 다음과 같은 특징을 지닌다.
- 전하를 포함하지 않은 닫힌곡면에서의 알짜 전기 선속은 0이다.

'고급물리학' 카테고리의 다른 글
| 【과학고전 읽어보기】 자연철학의 수학원리 - 소개 (0) | 2022.01.25 |
|---|---|
| 반사와 굴절 (0) | 2021.12.11 |
| 열역학 학습을 위한 열화학 기초 (0) | 2021.12.02 |
| 다차원 상의 운동 (0) | 2021.11.27 |
| 지진파 Seismic Wave – 지진파의 이해 (0) | 2021.11.26 |