
도함수 찾기 - 극한과 구간축소법
앞선 [02. 순간변화율의 계산 - 극한과 구간축소법]에서 배운 내용들을 시작으로, 어떤 함수의 순간 기울기인 도함수 개념을 이끌어 내보자.
- 구간축소법: 어떤 함수의 임의의 점에 대한 실질적인 함수의 변화율은 '구간에서의 평균 변화율'에서 x의 구간(Δx)을 더욱 좁혀나감으로써 f(x)의 한 점에서의 변화율 경향성을 예측할 수 있다. 두 구간의 가장 작은 차이를 증분이라 하고 기호로는 δx로 표현한다.
- 극한: 만약 x가 x축의 a라는 특정 값에 한없이 가까워질 때, 함수값 f(x)는 어떠한 극한 값을 가지게 되고 이를 L 이라는 수로 표현할 수 있는데, 구간축소법의 개념을 적용해 δx가 0에 가깝게 설정될 때, 극한의 기법을 활용하면 함수값 f(x)의 특정 극한 값 L을 구할 수 있다.
- 단, x가 a에 접근한다는 것이 x=a를 의미하는 것은 아니다.
3. SIM에 따른 미분의 정의
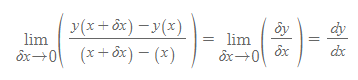
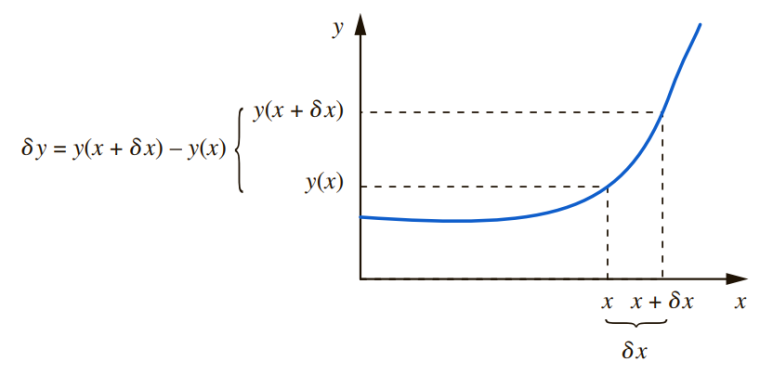
그림 1
구간축소법을 사용하여 y(x)의 미분값을 찾는 방법을 1차 원리에 의한 미분(differentiation from first principles)이라 한다.
y의 미분(derivative)
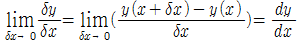
■
xy그래프에서의 y의 변화율을 y의 미분이라고 부르며, 증분 δx를 0으로 근사시킨 함수 그래프의 어떤 구간은 점으로 축소된다.
- dy/dx는 /dee y (by) dee x/로 읽는다.
- x는 독립변수, y는 종속변수이다.
- dy/dx는 간단하게 y'(prime)으로 표기하기도 한다.
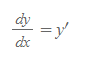
미분(differentiation)은 쉽게 말해 y에서 y'을 찾는 절차이다.
도함수 찾기 - 접선
SIM을 응용해, 접선의 정의 또한 유도할 수 있다.
- 할선(secant line): 곡선과 직선이 두 점에서 서로 만날 때 일반적으로 직선이 곡선을 자르는 모양을 갖는데, 이때의 '직선'을 곡선에 대한 '할선'이라 한다. 할선은 두 점에 대한 기울기로 SIM에서의 구간에서의 평균 변화율과 같다.
- 접선(tangent line): 곡선과 직선이 서로 한 점에서 만날 때, 이때의 '직선'을 곡선에 대한 '접선'이라 한다. 접선은 곡선 위 어떤 지점 a 근방에서의 할선 기울기의 극한 값으로, SIM에서의 한 점에서의 순간 변화율과 같다.
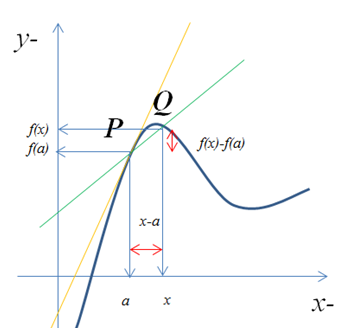
그림 2
[1] 할선의 기울기는 다음과 같다.

- 두 점 P, Q를 잇는 할선의 기울기
- 접선을 구하기 위해서는 점 Q가 곡선인 함수 f의 경로를 따라 P에 접근하도록 해야 한다.
[2] 점 Q를 점 P에 접근하도록 하되, x≠a이다.
[3] 접선이란, 곡선 위 어떤 지점 근방에서의 할선 기울기의 극한 값이다.
접선의 정의
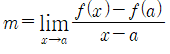
■
다시 말해 접선은 [그림 2]의 점 Q가 함수의 경로 f를 따라 P에 접근할 때 할선 PQ의 극한에서의 위치이다.
접선의 정의에서 x는 x≠a이므로, 미소 구간 h를 도입해 a+h라는 크기의 길이 값으로 바꿔 쓸 수 있다.
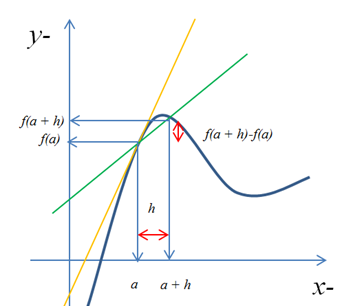
그림 3
같은 그래프임에도 이번에는 두 점을 a와 x 대신, a와 h(증분과 같은 개념)라는 새로운 수로 표현했다.
- h=x-a ⇒ 구간축소법에서 소개한 increment와 같다.
접선의 정의와 h의 정의를 접목하면, 접선의 일반식을 유도할 수 있다.
접선의 일반식
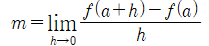
■
도함수 찾기 - 미분계수, 도함수
접선의 일반식은 변화율을 나타낼 때 매우 유용한 개념으로, 수학자들은 이후 여기에 특별한 명칭과 기호를 붙였다.
미분계수(derivative coefficient)

■
- a에서의 함수 f의 극한을 미분계수라 하고 f'(a)라고 표시한다.
- h→0의 필요충분조건은 x→a이다.
도함수(derivative)
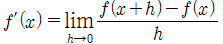
■
x지점에서 f'의 값은 기하학적으로 점 (x, f'(x))에서 f의 그래프에 접하는 접선의 기울기이다.
- f'(x)는 f의 derivative(of f)라는 새로운 함수로 정의된다.
- f'(x)의 정의역은 f의 정의역보다 크지 않다.
도함수는 모든 미분의 가장 근본적인 원리이다. 그러나 위의 계산과정은 너무나 많은 시간을 필요로 하고, 또한 복잡하다. 따라서 이런 수고를 덜기 위해 '미분법'을 공부해야 하고, 수많은 예제 풀이를 통해 패턴을 학습(및 암기)함으로써 미분을 기계적으로 할 수 있게 된다.
자주 사용되는 함수-미분 공식
미분은 다양한 함수에 대한 도함수를 구하는 과정으로, 다른 함수의 도함수 또한 같은 방식으로 유도되었다. 많이 사용되는 함수의 미분 공식은 예제를 풀이하면서 암기하도록 하자.

'미분적분학 > 미분' 카테고리의 다른 글
| [대학수학 - 미분적분학] 07. 다항함수의 도함수 (0) | 2023.08.23 |
|---|---|
| [대학수학 - 미분적분학] 06. 극한의 부정형 계산과 로피탈의 정리 (예제 포함) (0) | 2023.08.20 |
| [대학수학 - 미분적분학] 05. 극한의 성질 (0) | 2023.08.19 |
| [대학수학 - 미분적분학] 03. 심화 - 입실론-델타(엡실론-델타) 논법 (0) | 2023.08.17 |
| 【공업수학】 미분방정식과 모델링 (0) | 2022.03.12 |