
미분방정식(differential equation): 미지 함수의 도함수를 포함한 방정식으로 미지의 함수 f(x)와 그 도함수 간의 관계성을 나타냄
① 상미분방정식(ordinary differential equation; ODE): 한 개의 변수에 의존하는 미분방정식
② 편미분방정식(partial differential equation; PDE): 여러 개의 변수에 의존하는 미분방정식
모델링(modeling): 관찰한 물리적 상태를 수학적 모델(mathematical model)로 전환하는 일반적인 과정
Mathematical modeling refers to the process of creating a mathematical representation of a real-world scenario to make a prediction or provide insight.
모델링
수학적 모델링(mathematical modeling, modeling): 공학적 문제의 모델(model)을 세우고, 그것을 수학적으로 풀며, 마지막으로 이를 물리적으로 해석하는 일련의 과정
- Mathematical Modeling으로부터 도출된 Model은 물리학의 많은 개념이 도함수로 표현되므로, 미지함수의 도함수를 포함함 ⇒ Model로서 Differential Equations
미분방정식의 구분
미지함수가 1변수 함수 또는 다변수 함수인지에 따라, (1)상미분방정식과 (2)편미분방정식으로 분류
|
구분
|
내용
|
|
ODE
|
미지함수의 도함수를 포함한 방정식
- 1개의 독립변수 x와 1개 이상의 종속변수 y의 도함수만을 포함
|
|
PDE
|
미지함수의 편도함수를 포함한 방정식
- 2개 이상의 독립변수(x, y, ...)와 1개 이상의 종속변수 u의편도함수를 포함
예: 열전도 방정식, 파동방정식
|
만약 미지함수 y의 n계 도함수가 방정식에서 가장 높은 계수의 도함수이면, 이 상미분 방정식은 n계(order n)라고 함
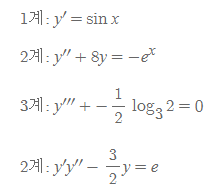
여기서 y'=dy/dx, y''=d^2(y)/d(x^2)임
1계 미분방정식(first order DE): 최고계 미분항이 1계 미분인 미분방정식
2계 미분방정식(second order DE): 최고계 미분항이 2계 미분인 미분방정식
1계 미분방정식 Vs. 2계 미분방정식
1. 1계 미분방정식의 표현
① 음함수형(implicit form) 표현
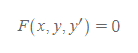
② 양함수형(explicit form) 표현
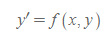
2. 2계 미분방정식의 표현
① Implicit Form
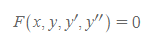
② Explicit Form
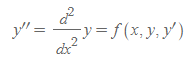
미분방정식의 해
해(solution): 만약 함수 h(x)가 어떤 열린구간 a<x<b에서 정의되고, 미분가능하며, y, y'을 각각 h, h'으로 대체할 때 식 F(x, y, y')=0이 항등식이 되는 경우, 함수 y=h(x)를 구간 a<x<b에서의 주어진 상미분방정식의 해라 함
A function y=h(x) is called a solution of a given ODE F(x, y, y')=0 on some open interval a<x<b if h(x) is defined and differentiable throughout the interval, and is such that the equation becomes an identity if y and y' are replaced with h and h' respectively.
미분방정식의 해 또는 해 함수는 미분방정식에 대입하였을 때 항등적으로 만족시키는 Solution 또는 함수를 의미
- 미분방정식의 풀이는 미분방정식을 항등적으로 만족하는 독립변수의 함수를 구하는 것

미분방정식의 해 종류
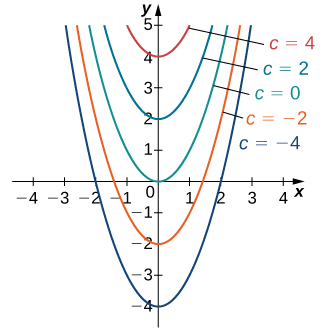
① 일반해(general solution): 미분방정식을 만족하는 모든 해
- 각 상미분방정식은 임의의 상수 c를 포함하는 데 이 상수를 포함한 해를 General Solution이라 함
- 해의 복소수 식을 피하기 위해 구간으로 제한되기도 함
② 특수해(particular solution): 주어진 미분방정식을 만족하는 유일한 해
- 일반해에 포함된 임의의 상수 c에 구체적인 값을 지정하고, 유일하게 얻을 수 있는 해
- 임의의 상수에 주어진 조건을 대입하여 적분 상수 c가 없음
- 미분방정식과 초기조건(initial condition)을 동시에 모두 만족하는 해
③ 특이해(singular solution): 일반해로부터 얻어질 수 없는 특이한 해
- 일반해에 어떠한 임의의 상수를 지정하여도 얻어질 수 없음
- 일반해로부터 표현이 불가능
- 미분방정식으로부터 얻을 수 없음
'미분적분학 > 미분' 카테고리의 다른 글
| [대학수학 - 미분적분학] 07. 다항함수의 도함수 (0) | 2023.08.23 |
|---|---|
| [대학수학 - 미분적분학] 06. 극한의 부정형 계산과 로피탈의 정리 (예제 포함) (0) | 2023.08.20 |
| [대학수학 - 미분적분학] 05. 극한의 성질 (0) | 2023.08.19 |
| [대학수학 - 미분적분학] 04. 한 점에서의 변화율과 도함수 (0) | 2023.08.18 |
| [대학수학 - 미분적분학] 03. 심화 - 입실론-델타(엡실론-델타) 논법 (0) | 2023.08.17 |