728x90
반응형

극한 법칙
Limit Laws
극한을 알고 있는 함수들의 대수적 결합함수의 극한 계산을 위해, 아래의 성질들을 이용할 수 있다.
극한법칙(Limit Laws)
c가 상수이고, 두 극한 lim_x→a[f(x)], lim_x→a[g(x)]가 존재할 때, 다음의 성질을 만족한다.

■
또한 극한법칙의 계산 수행 과정에서 아래의 기본극한값(basic limit result)을 활용해야 한다.
기본극한값(Basic Limit Result)

■
첫 번째 극한값은 y=c 그래프를, 두 번째 극한값은 y=x 그래프를 그리면 그 이유를 쉽게 알 수 있다.
직접대입성질
- f가 다항식이거나 유리함수이고, a가 f의 정의역 내에 존재하면 다음의 성질을 이용할 수 있다.

여러가지 극한법칙과 직접대입성질을 이용하면 다항함수와 유리함수의 극한 계산을 매우 간단하게 할 수 있다.
- 다항함수의 극한 계산을 위해 함수의 식에서 x 대신 a를 대입한다.
- 분모가 0이 되지 않는 경우에 한하여, 유리함수의 극한을 계산하기 위해 함수의 식에 x대신 a를 대입할 수 있다.
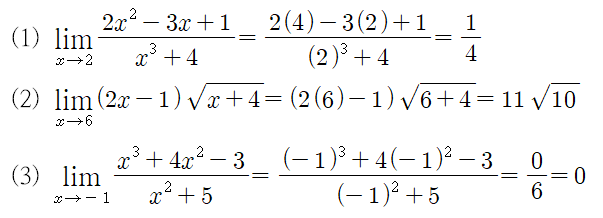
다항함수의 극한
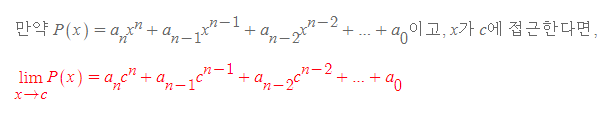
유리함수의 극한

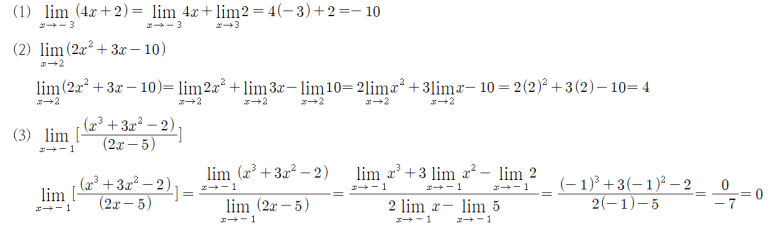
약분과 유리화
예를 들어 아래와 같은 극한의 계산을 한다고 해보자.
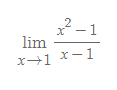
극한의 성질을 이용하여 a에 x=1을 바로 대입하면 안된다. 왜냐하면 분모의 자리에 1을 대입하면 분수에서 0을 나누는 불가한 상황이 발생하기 때문이다. 대신 x^2-1을 적절히 처리하여 f(x=1)이 정의될 수 있는 함수로 고칠 수 있다.
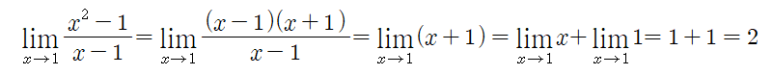
다음 제곱근이 들어간 극한의 계산을 해보자.

극한의 성질을 이용하면 a에 y=0을 바로 대입하면 안되는데, 제곱근이 들어간 경우는 유리화 과정을 통해 직접대입성질을 응용할 수 있다.
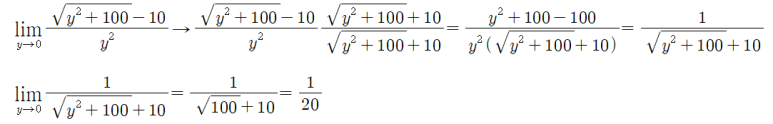
같은 방식으로 아래 극한 식을 풀어보자.
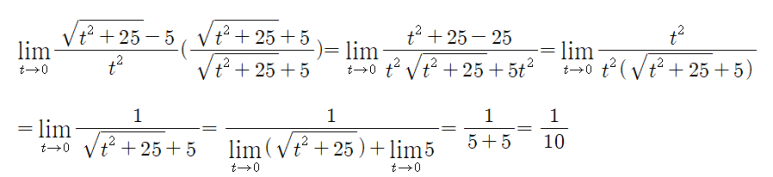
728x90
반응형
'미분적분학 > 미분' 카테고리의 다른 글
| [대학수학 - 미분적분학] 07. 다항함수의 도함수 (0) | 2023.08.23 |
|---|---|
| [대학수학 - 미분적분학] 06. 극한의 부정형 계산과 로피탈의 정리 (예제 포함) (0) | 2023.08.20 |
| [대학수학 - 미분적분학] 04. 한 점에서의 변화율과 도함수 (0) | 2023.08.18 |
| [대학수학 - 미분적분학] 03. 심화 - 입실론-델타(엡실론-델타) 논법 (0) | 2023.08.17 |
| 【공업수학】 미분방정식과 모델링 (0) | 2022.03.12 |