
상수함수
모든 함수 중 상수함수는 가장 간단한 함수의 형태로 다음과 같이 그래프가 나타난다.
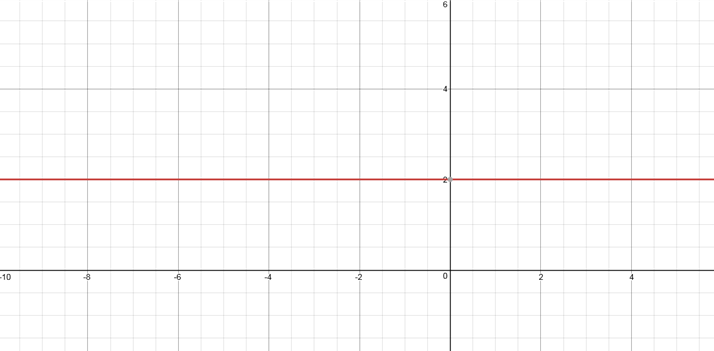
상수함수는 y=c의 꼴로 c는 상수(constant)를 뜻한다. 이 상수함수의 도함수는 아래 식과 같다.
상수함수의 도함수 Constant Rule
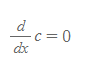
■
상수함수의 도함수는 다음과 같이 증명된다.
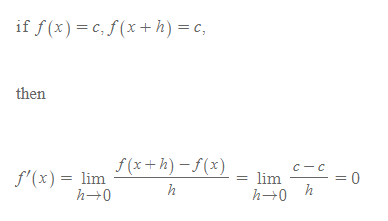
□
거듭제곱함수
함수 f(x)=x^n의 n이 양의 정수를 가질 때를 생각해보자. 만약 n=1이라면 f(x)=x^1=1이고, 그래프는 f(x)=x=1의 직선형태로 나타날 것이다.
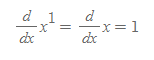
다음 n이 2, 3일 때를 생각해보자.
1) if n=2
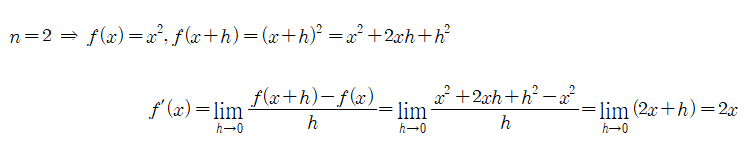
□
2) if n=3
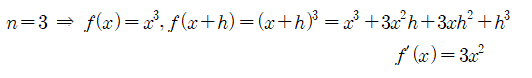
□
위의 연산을 반복하면 우리는 어떠한 규칙을 얻을 수 있는데, n이 양의 정수일 때 거듭제곱함수의 도함수는 다음과 같다.
양의 거듭제곱 법칙
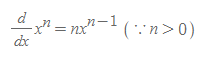
■
양의 거듭제곱 법칙은 이항정리 식(x+h)^n을 lim에 대입함으로써 증명할 수도 있다.
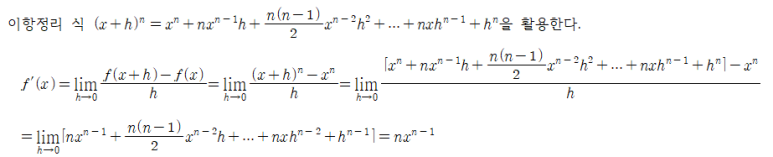
한편 음의 정수를 지수로 갖는 거듭제곱의 도함수의 경우에도, 거듭제곱 법칙이 마찬가지로 성립한다. 따라서 음의 거듭제곱 법칙을 양의 것과 결합하여 일반적인 거듭제곱 법칙을 다음과 같이 표현할 수 있다.
거듭제곱 법칙 - 거듭제곱함수의 도함수
만약 n을 임의의 실수라 하면, 거듭제곱함수의 일반형은 다음과 같다.
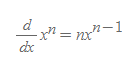
■
거듭제곱함수의 도함수의 몇 가지 예제를 살펴보자.
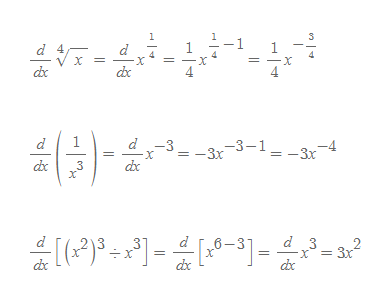
거듭제곱 법칙을 이용하면 점 (x, y)에서 접선의 방정식과 법선의 방정식을 매우 쉽게 구할 수 있다.
접선의 방정식

■
법선의 방정식

■
새로운 도함수 구하기
새로운 함수가 이전의 함수들을 더하거나, 빼거나, 또는 상수배를 하여 만든 것이라면, 그 도함수는 이전 함수들의 도함수로부터 계산된다.
- 상수배 법칙: 어떤 함수의 상수 배(multiplication)를 한 함수의 도함수 구하기
- 합 법칙: 두 함수 이상의 함수를 더한 합성 합수의 도함수 구하기
- 차 법칙: 두 함수 이상의 함수를 뺀 합성 함수의 도함수 구하기
상수배 법칙 Constant Multiple Rule
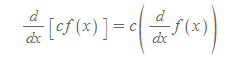
■

□
합 법칙 Sum Rule

■
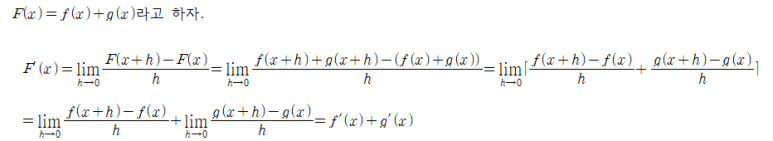
□
차 법칙 Difference Rule
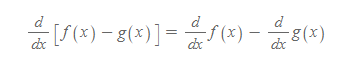
■
'미분적분학 > 미분' 카테고리의 다른 글
| [대학수학 - 미분적분학] 09. 지수함수의 도함수 (0) | 2023.08.24 |
|---|---|
| [대학수학 - 미분적분학] 08. 곱미분과 몫미분 (0) | 2023.08.24 |
| [대학수학 - 미분적분학] 06. 극한의 부정형 계산과 로피탈의 정리 (예제 포함) (0) | 2023.08.20 |
| [대학수학 - 미분적분학] 05. 극한의 성질 (0) | 2023.08.19 |
| [대학수학 - 미분적분학] 04. 한 점에서의 변화율과 도함수 (0) | 2023.08.18 |