[대학수학 - 미분적분학] 09. 지수함수의 도함수

잉글랜드의 수학자 오트레드(William Oughtred, 1574~1660, 잉글랜드)의 초상화와 그가 저술한 『수학의 열쇠 Clavis Mathematicae』(1631)

 

 

 

자연로그 밑 e

 

자연로그 밑(natural constant) e는 어떤 로그의 밑이 극한값 식 1로 정의될 때의 밑을 의미하며, 실수 중 무리수에 속하는 초월수(transcendental number; 계수가 유리수인 어떤 다항 방정식의 해도 될 수 없는 복소수)로 분류된다. 약 2.71828로 근사되는 수로 극한값으로 다음과 같이 표현된다.

 

식 1

 

u=1/n으로 치환한다면, n→∞일 때 1/n→0이고, e를 식 2로 재정의 할 수 있다.

 

식 2

 

그래프 표현

 

함수 f(x)=(1+x)^1/x의 그래프에서 불연속점 (0, e)를 확인할 수 있다.

 

 

f(x)=(1+1/x)^x의 그래프에서 점근선 y=e로 나타난다.

 

 

e의 역사

무리수 e가 최초로 기록된 것은 1618년 존 네이피어(John Napier, 1550~1617, 스코틀랜드)에 의해서이다. 하지만 그는 로그표를 작성하던 중 여러 가지 계산의 결과 값 중 하나로 e를 다루었을 뿐 오늘날처럼 상수로 취급하진 않았다. 후일 오트레드의 저서 『수학의 열쇠』를 통해 네이피어의 로그표가 널리 보급되면서 e의 존재가 함께 소개되지만 그 역시 저서에서 e를 특별한 상수로 취급하지 않았다.

Jakob Bernoulli (1655~1705)

 

e를 상수로 간주한 최초의 인물은 스위스의 수학자 야코프 베르누이(Jakob Bernoulli, 1655~1705, 스위스)이며, 그는 무한급수(infinite series)의 형태로 e를 정의했다.

 

 

Christiaan Huygens (1629~1695, 네덜란드) / Leonhard Euler (1707~1783)

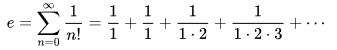
베르누이가 급수의 형태로 정의한 무리수 e는 이후 라이프니츠와 네덜란드의 수학자 하위헌스에 의해 처음에는 'b'로 간단히 표기됐다.

그러다 자연로그 밑이 개념적으로 정착되면서, 스위스의 수학자 오일러(Leonhard Euler, 1707~1783, 스위스)는 무리수를 'e'로 쓰기 시작했고(1727~1728), 이후 자신의 저서 『Mechanica, 메카니카』(1736)에서는 공식적으로 자연로그 밑을 'e'로 작성했다.

 

지수함수

 

지수의 기본성질

 

■

 

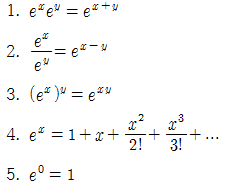
여기서 e의 정의는 다음과 같다.

 

 

e의 정의

 

도함수의 정의를 이용해 f(x)=a^x의 도함수를 구해보자.

 

 

증명 과정에서, 지수함수의 변화율 f'(x)은 함수 자신(a^x)에 비례함을 알 수 있다.

 

 

밑 a가 취할 수 있는 선택 가능한 값들 중 가장 간단한 미분식은 f'(0)=1일 때다. a가 2, 3인 경우에 대해 f'(0)을 각각 구했으므로, f'(0)=1을 만족하는 수 a는 2와 3 사이에 위치함을 유추할 수 있다.

 

더 연산하면, e는 약 2.71828...로 계산된다.

- 기하학적으로 f(x)=e^x는 (0, 1)에서 접선의 기울기 f'(0)=1인 함수이다.

□

지수함수의 도함수는 크게 3가지로 설명할 수 있다.

 

 

자연지수함수의 도함수

 

■

 

밑이 a>0인 지수함수의 도함수

 

■

 

참고로, 밑이 a>0인 지수함수의 도함수는 연쇄법칙을 활용해 유도한 결과이다.