
미분의 여러 가지 내용을 증명하는 데 삼각함수의 극한 값들이 중요하게 활용된다.
사인 함수
sinx의 극한

식 1
-|x|≤sinx≤|x|이므로, squeeze theorem을 이용하면, 식 1이 성립함을 확인할 수 있다.

sinx/x의 극한

식 2
x 값을 극도록 줄일수록 0.999...로 계산된다.
sinπ/x의 극한
존재하지 않는다.
x^2(sin(1/x))의 극한
부등식의 관계 -1≤sin(1/x)≤1에 x^2을 곱하면,

식 3
식 3을 얻을 수 있다.

식 4
식 4에 근거해, 식 3에 squeeze theorem을 적용하면, x^2(sin(1/x))은 0이라 할 수 있다.

코사인 함수
cosx의 극한

모든 x에 대해 0≤1-cosx≤|x|이므로, lim_{a→0}(1-cosx)=0이 성립하고, 극한법칙에 따라 lim_{a→0}cosx=1(식 5)을 유도할 수 있다.

식 5
cosx-1/x의 극한

탄젠트 함수
tanx/x의 극한

이외에도,

와 같은 탄젠트 함수 관련 극한 값들이 있다.
무한소
infinitesimal
x→a일 때,
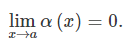
식 1
식 1의 함수 α(x)를 무한소(infinitesimal)라고 부른다.
x→a의 조건에서 α(x)와 β(x)를 무한히 작은 크기의 함수라고 할 때, 다음 4가지 극한의 특성을 알아보자.
1.
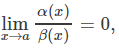
then we can say that the function α(x) is an infinitesimal of higher order than β(x).
2.
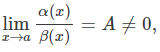
then, the function α(x) and β(x) are called the infinitesimals of the same order.
3.
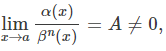
then, the function α(x) is called an infinitesimal of order n compared with the function β(x).
4.
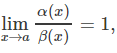
then, the function α(x) and β(x) are said to be equivalent as x→a.
특히 두 개의 무한소 비(ratio of two infinitesimals as x→0 or a)의 극한을 계산할 때, 아래의 표는 극한의 계산을 더 쉽게 만들어 준다.

표 1
EXAMPLE 1.
다음 식을 구하시오.
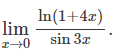
SOLUTION.
표 1에 근거해, ln(1+4x)는 4x로 sin3x는 3x로 근사시킬 수 있다.
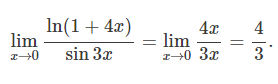
■
EXAMPLE 2.
다음 식을 구하시오.
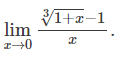
SOLUTION.
3√1+x는 (1+x)^1/3으로 고쳐 쓸 수 있고, 표 1에 근거해 1+x/3으로 근사시킬 수 있다.
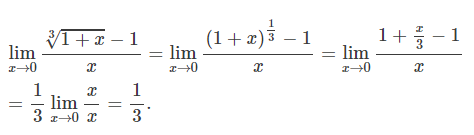
■
EXAMPLE 3.
다음 식을 구하시오.
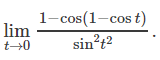
SOLUTION.
- 1-cosx는 x^2/2로 근사할 수 있다.
- sinx는 x로 근사할 수 있다.
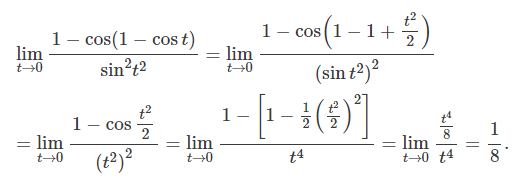
■
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 2. 함수의 변화율 (0) | 2024.11.07 |
|---|---|
| 【미분적분학 1】 Chapter 1. 함수와 접선 (0) | 2024.11.06 |
| [대학수학 - 미분적분학] 09. 지수함수의 도함수 (0) | 2023.08.24 |
| [대학수학 - 미분적분학] 08. 곱미분과 몫미분 (0) | 2023.08.24 |
| [대학수학 - 미분적분학] 07. 다항함수의 도함수 (0) | 2023.08.23 |