Herald-Lab
【미분적분학 1】 Chapter 1. 함수와 접선 본문

미분적분학(calculus): 미적분학, 함수로 표현할 수 있는 어떠한 물리량의 '변화'를 분석하는 데 사용되는 수학기법
- 함수(function): 어떠한 집합 X, Y에 대한 함수 f란, 아래를 만족하는 대응관계로 정의한다. [그림 1]
- 임의의 원소(element) x에 대해 그에 대응하는 원소 y가 유일하게 존재한다. 이때 원소 x는 집합 X에 속하고, 원소 y는 집합 Y에 속한다.
- 집합 X는 정의역(domain), 집합 Y는 공역(codomain)이다.
- 원소 x에 대응되는 원소를 x의 함수값(value of a function) 또는 상(image)이라 한다. 함수값은 f(x)로 표기한다.
- 치역(range): 모든 함수값을 모은 집합으로 f(X)로 표기한다.
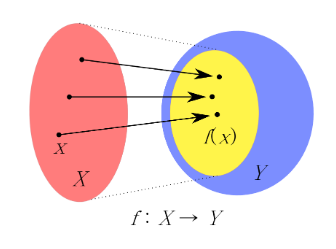
즉, 함수 f란, 집합 X의 각 원소 x를 집합 Y에 있는 오직 한 원소 f(x)에 대응시키는 규칙을 뜻한다.
특히 실세계를 반영하는 물리학의 세계에서 어떤 양의 변화는 또 다른 양의 변화와 연관이 있다. 이탈리아의 물리학자이자 천문학자였던 갈릴레오(Galileo Galilei, 1564-1642)는 물체가 떨어지는 거리가 시간의 제곱에 비례한다[표 1]는 사실을 발견했다.

- 시간에 따른 변화(change over time) 등 물리학적 변화에 있어, 원소 x는 독립변수(independent variable)이다.
- 그리고 함수값 또는 상 f(x)는 종속변수(dependent variable)이다. [그림 2]
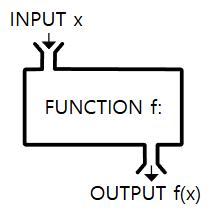
x, y축이이 놓인 그래프에서 정의역과 치역, 그리고 원소(종속변수)와 함수값(독립변수)은 [그림 3]과 같이 나타난다.
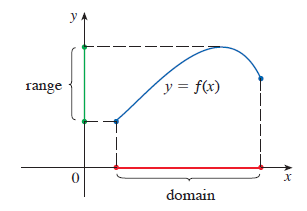
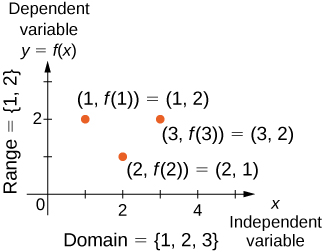
y축의 수는 x축의 원소에 의한 함수값 또는 상과 동일[그림 4]하다.
할선과 접선
Secant Line and Tangent Line
할선(secant line): 곡선을 한 번 이상 만나는 직선, 두 점을 잡고 지나는 선
- 할선의 기울기를 구하는 식을 통해 접선의 기울기를 추론할 수 있다.
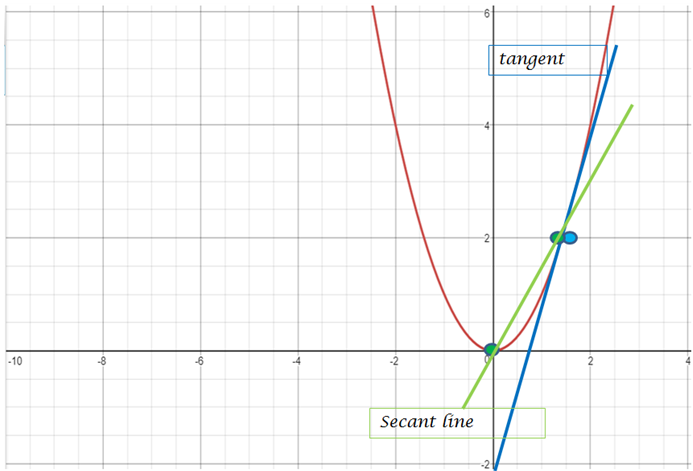
[그림 5]와 같이 secant line은 곡선에 '두 점'을 지나는 반면, 접선(tangent line)은 '한 점'만 접하는 데, 이는 접선이 곡선과 접하는 직선으로 접점에서 곡선과 같은 방향을 갖기 때문이다. 여기서 곡선은 y=x^2이다.
접선(tangent line): 곡선과 접하는 직선으로 접점에서 곡선과 같은 방향을 갖는다.
할선의 기울기
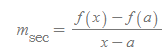
■
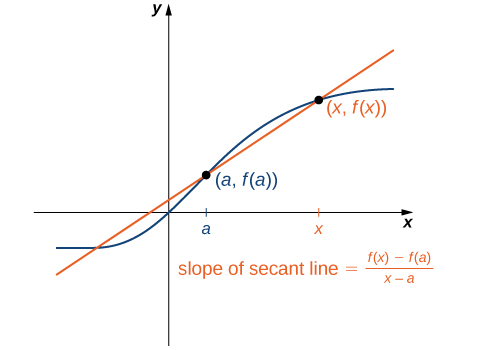
할선은 두 개의 서로 가까운 점을 설정([그림 6]의 두 점)하여 '기울기' 값으로 구할 수 있다.
접선 만들기
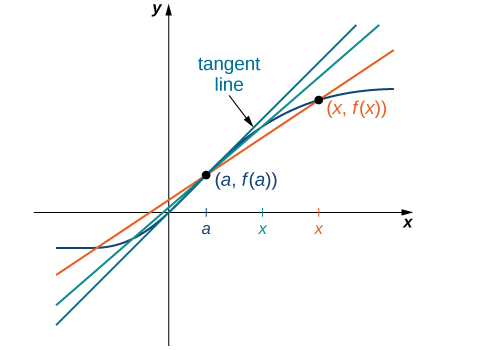
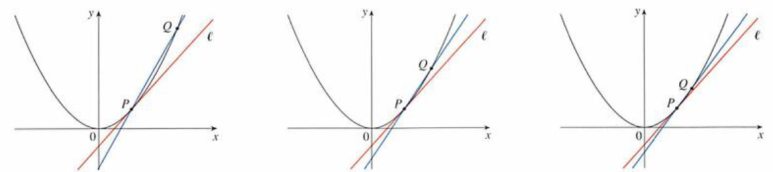
할선의 기울기는 두 개의 점을 설정한 뒤, 기울기를 구하는 공식으로 구할 수 있다. 그러나 접선은 '접점(서로 접하는 한 점으로 표현되는 구역)'에서 곡선과 같은 방향으로 난 직선으로, 일반적인 기울기 식으로는 그 값을 구할 수 없다. 단, 할선의 두 점을 P, Q라 했을 때, P점을 고정시킨 뒤, Q점을 P점에 가깝게 나타낼수록 기울기는 어떠한 특정한 값을 향한다.
- 특정한 값으로 향할 때의 그 경향성을 접선의 기울기[그림 7]라 하고, 이는 할선의 기울기 극한으로 정의한다.
접선의 기울기 식은 극한을 배웠다 가정하면, 아래와 같이 쓴다.
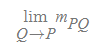
- 할선의 두 점 P, Q 중, Q점을 P점에 가깝게 나타낸 것[그림 8]을 Q→P라 표현한다.
- m_PQ는 할선의 기울기로 Q점이 P점을 향해 다가가나 두 점 자체가 여전히 독립적으로 존재함을 나타낸다.
예를 들어, P를 (1, 1)로 Q를 (1.5, 2.25)로 두었을 때 m_PQ는 아래와 같이 계산된다.
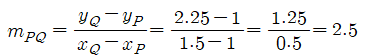
그리고 Q를 P점에 가까이 하기 위해 Q를 (1.01, 1.0201), (1.001, 1.002001) 등으로 줄였을 때, m_PQ는 다음과 같이 계산된다.
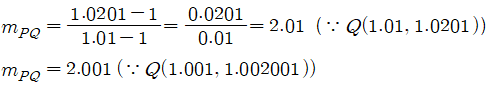
m_PQ는 2라는 수의 경향성을 따르고 있고, 이것이 접선의 기울기이다.
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 3. 극한과 구간축소법 (0) | 2024.11.08 |
|---|---|
| 【미분적분학 1】 Chapter 2. 함수의 변화율 (0) | 2024.11.07 |
| [대학수학 - 미분적분학] 10. 삼각함수의 극한과 무한소 (0) | 2023.08.31 |
| [대학수학 - 미분적분학] 09. 지수함수의 도함수 (0) | 2023.08.24 |
| [대학수학 - 미분적분학] 08. 곱미분과 몫미분 (0) | 2023.08.24 |




