
극한 개념의 발전
History of the Concept of Limits

독일의 수학자 헤르만 헹켈(Hermann Hankel, 1839-1873)에 따르면, 현대적인 극한의 개념은 유클리드 원론 제10권 첫 번째 명제(X.1)에서 비롯되었으며, 이는 유클리드와 아르키메데스의 소진법(method of exhaustion)에 기초가 된다.
"Two unequal magnitudes being set out, if from the greater there is subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process is repeated continually, then there will be left some magnitude less than the lesser magnitude set out."
두 개의 크기가 다른 양이 존재할 때, 더 큰 양에서 그 절반보다 더 큰 부분을 빼고, 남은 양에서도 다시 절반보다 더 큰 부분을 계속해서 빼면, 나머지 작은 양보다 더 작은 값을 갖게 된다.
위는 원론에서 언급한 소진법에 의한 극한 값의 직관적인 해석이다.
예를 들어 두 개의 양(magnitude)이 존재하고 하나는 큰 양(100), 하나는 작은 양(1)이라 가정하자. 큰 양 100에서 절반보다 큰 부분을 빼나간다고 할 때 절반보다 큰 부분을 60이라 가정하면 100-60에 40이 남는다. 다음 40에서 절반보다 큰 부분 25를 가정하면 40-25=15가 남는다. 남은 15에서 또 절반보다 큰 8을 가정하면 15-8=7이 남고 이런 식으로 계속하면 어느 순간 작은 양(1)보다 더 작은 값을 갖게될 것이다.
- 극한은 어떠한 작은 양 값보다도 더욱 작은 값을 가질 수 있다.
- 소진법은 무한히 위와 같은 방식으로 '반복가능'하다.

이후 플란더스 지방의 수학자이자 예수회 성직자였던 그레고리우스(Gregoire de Saint-Vincent, 1584-1667)는 1647년 자신의 저서인 『Opus Geometricum』에서 처음으로 기하급수의 극한계(terminus)를 언급한다.
- 극한계의 정의: 수열의 극한계란, 해당하는 수열의 끝인데 이 수열이 무한히 진행된다고 해도 절대로 도달할 수는 없으나, 주어진 값에는 무한히 가까워질 수 있다.
"The terminus is the end of the series, which none progression can reach, even not if she is continued in infinity, but which she can approach nearer than a given segment."

현대적인 극한의 정의는 1817년 체코의 수학자 베르나르 볼차노(Bernard Bolzano, 1781-1848)가 고안했다. 그러나 그의 연구는 사후 30년이 지난 이후에 다른 수학자들에 알려졌는데, 이후 미분적분학 교과서에서 극한의 엄밀한 정의는 프랑스의 수학자 오귀스탱-루이 코시(Augustin-Louis Cauchy, 1789-1857)와 독일의 수학자 칼 바이어슈트라스(Karl Weierstrass, 1815-1897) 등을 통해 발전된 개념으로 소개된다.
특정한 점에서의 변화율
Rate of Change at a Specific Point
이전 챕터에서 우리는 함수의 변화율을 (1)현과 (2)접선의 기울기로 학습했다. 지금부터는 임의의 점에 대한 실질적인 함수의 변화율을 구해보자.

[그림 1]의 함수는 다음 식으로 표현된다.

그리고 구간 [3,4]에서 변화율을 다음과 같이 구할 수 있다.

마찬가지로, 어떤 특정한 점에서의 함수의 변화율을 구하기 위해서는 그 점에 최대한 근접한 구간의 기울기를 구함으로써 풀 수 있다. 따라서 그 구간을 [3,3.1], [3, 3.01]... 로 계속 줄여나가면 된다.
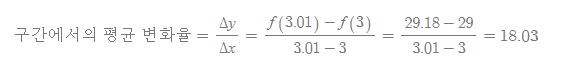
구간에서의 평균 변화율을 계속 계산하다보면 18로 다가가는 경향성을 확인할 수 있다.
구간축소법
Shrinking Interval Method(SIM)
위 문제는 구간축소법(Shrinking Interval Method, SIM)이라는 기법을 소개하는 대표 예제로, 어떤 특정한 점에서의 함수의 기울기를 구하기에 매우 직관적인 형태를 갖는다.
- x축의 특정 구간의 축소를 하지만 그 구간 자체가 어떠한 한 점으로 완전하게 일치하지 않음에 유의한다. 즉, 구간의 길이는 아무리 줄이더라도 그 길이가 미소하게라도 존재함을 가정한다. ⇒ 소진법 참고
- 가장 작은 미소 구간 또는 그 두 구간 지점의 차이를 증분(increment)이라 하고, 기호로는 δx로 표기한다.
구간의 increment를 도입한 후 x=3에서 f(x)=3x^2+2의 변화율을 구해보자.
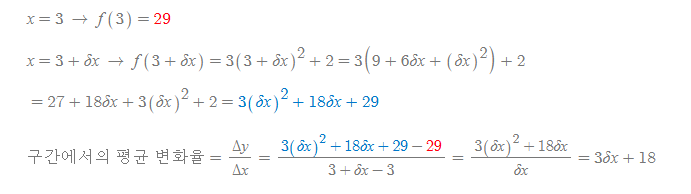
특정한 지점의 기울기는 (1)x축의 특정 구간(δx)의 최대한 축소를 통해 구해지며, 극한의 정의를 빌리자면 (2)δx값이 0에 가까워질수록 그 기울기 값은 정확해지기 때문에, δx를 0이라 가정하여,
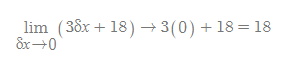
로 최종 계산할 수 있다.
SIM에서 구간축소란, 결국 y축의 어떠한 특정한 점 극한 값 L을 구하기 위해 x축의 주어진 구간을 최대한 줄이는 과정이다.
SIM기법을 활용한 일반적인 한 지점에서의 변화율
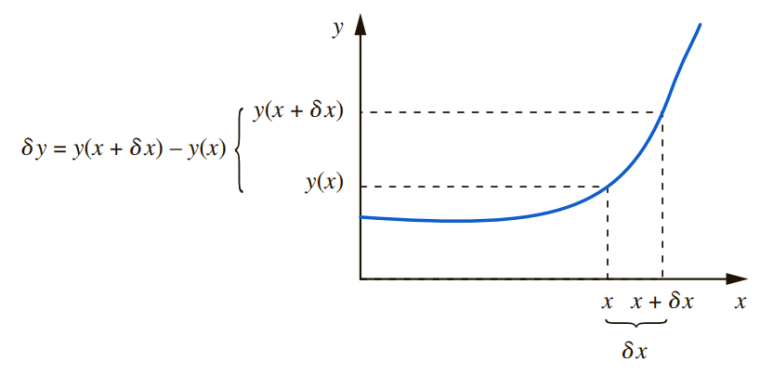
x에 관한 함수 y=f(x)에서, 일반적인 지점 x에 대한 y의 변화율을 계산하고자 한다.
- 구간 [x,x+δx]에서 y의 변화량은 y(x+δx)-y(x)이다. 또한 x축의 구간 길이는 (x+δx)-x다.
- 평균변화율은 Δy/Δx이므로 이를 적용하면 다음과 같이 식이 전개된다.
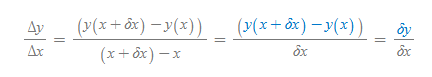
특별히, δy가 계산된 배경([그림 2])에 주목하자.
SIM에서 특정한 지점의 기울기는 결국 δx→0일 때 가장 근사치로 계산되어지므로,
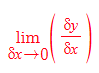
로 표현이 가능하다.
SIM에 따른 미분의 정의
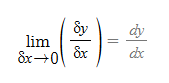
■
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 5. 극한값의 필요충분조건 (0) | 2024.11.10 |
|---|---|
| 【미분적분학 1】 Chapter 4. 도함수 찾기 (0) | 2024.11.09 |
| 【미분적분학 1】 Chapter 2. 함수의 변화율 (0) | 2024.11.07 |
| 【미분적분학 1】 Chapter 1. 함수와 접선 (0) | 2024.11.06 |
| [대학수학 - 미분적분학] 10. 삼각함수의 극한과 무한소 (0) | 2023.08.31 |
