
극한의 정의
Definition of Limits
극한값(극한)이 존재할 수 있는 필요충분조건을 공부하기 위해, 앞선 챕터에서 다룬 극한의 정의를 다시 한 번 정리한다.
극한의 일반적인 정의는 다음과 같다.

x가 a에 접근할 때, f(x)의 값은 L에 가까워지는데, 이때 x≠a임에 유의한다.
- x를 a에 접근할 때, x=a는 고려하지 않는다. a의 근방에서 함수 f가 어떻게 정의되는 지가 극한 개념의 핵심이다.
구간축소법을 활용해 도함수를 찾는 과정[그림 1]에서 극한은 아래와 같이 이용되었다.


어떠한 그래프 상에서 특정한 지점의 접선을 구할 때, [그림 2]와 같이 x 대신 a, δx 대신 h로 바꾸어 표현하는데, 이때 접선의 일반식은 아래와 같다.


이때 a는 x축에 놓여진 임의의 수로 다시 a를 x로 바꾸어 쓰면, 도함수의 일반식을 아래와 같이 나타낼 수 있다.

EXAMPLE. 극한의 정의

SOLUTION.
x에 2에 접근하는 수들로 대입한다.

표의 x값은 모두 2에 가까워지는 수들의 집합으로 f(x)는 점차 4로 수렴함을 확인할 수 있다.
■
EXAMPLE. 극한의 정의 (2)
아래의 극한 값을 구하시오.

SOLUTION.
위의 예제(극한의 정의)와 같이 표를 작성하여 풀면, 첫 번째는 0.5, 두 번째는 1/6의 값으로 접근함을 알 수 있다.
- 단, 계산기의 소수점 계산 한계 때문에 두 번째의 결과가 0처럼 수렴하는 것으로 보일 수 있다.
■
EXAMPLE. 극한값의 추론
함수 f(x)에 대해 x=0은 정의되지 않고, x에 접근하는 값에 근사하는 몇 개의 작은 수치를 대입해 함숫값을 구하면 아래와 같다.

이와 같이 계속 풀어가면 극한 값은 0으로 접근한다고 추론할 수 있는데, '그러나' 실제 그래프는 아래와 같이 나온다.
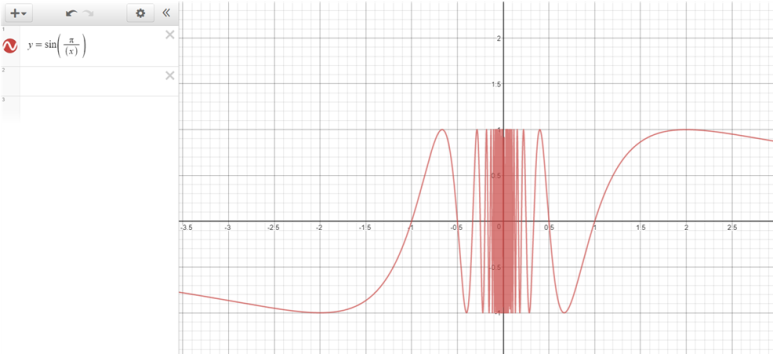
x가 0으로 접근할 때, f(x)의 값은 어떠한 특정 수에 접하지 않으므로, 위의 극한값은 존재하지 않는다라고 할 수 있다. ⇒ +1과 -1 사이에서 값은 '진동'한다.
■
극한의 방향성
Direction of Limits
극한값의 추론 예제에서 극한의 정의에는 함정이 있음을 보인다. 부적절한 x값을 사용했을 때, 잘못된 극한을 추론할 수도 있고, 때론 언제 계산을 멈춰야하는 지도 판단하기 어렵다.
좌극한과 우극한 | Left-hand Limits and Right-hand Limits
좌극한(limit from the left, left-hand limit)[그림 3]: a보다 작으면서 a에 충분히 가깝도록 x를 설정하면, f(x)의 값이 L에 가까워지는 데, 이 때 x→a인 경우, f(x)의 좌극한은 L이라 한다.
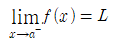
우극한(limit from the right, right-hand limit)[그림 3]: a보다 크면서 a에 충분히 가깝도록 x를 설정하면, f(x)의 값이 L이 가까워지는 데, 이 때 x→a인 경우, f(x)의 우극한은 L이라 한다.
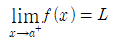
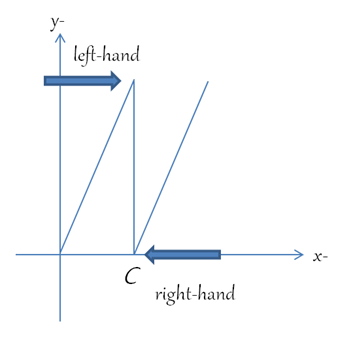
좌극한과 우극한은 [그림 3]과 같이 C를 향한다는 공통점 때문에 일방향 극한(one-sided limit)으로 묶어 부르며, 좌극한은 그래프의 '왼쪽'에서 출발하여 오른 방향으로 움직이며, 우극한은 '오른쪽'에서 출발하여 왼 방향으로 움직인다.
일방향성 극한을 정의했고, 이 둘을 이용하면 극한의 필요충분조건을 정의할 수 있다.
극한(값)의 필요충분조건
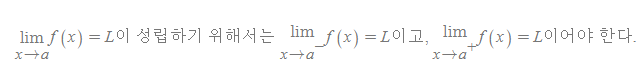
■
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 7. 극한의 성질 (0) | 2024.11.12 |
|---|---|
| 【미분적분학 1】 Chapter 6. 함수의 연속성 (0) | 2024.11.11 |
| 【미분적분학 1】 Chapter 4. 도함수 찾기 (0) | 2024.11.09 |
| 【미분적분학 1】 Chapter 3. 극한과 구간축소법 (0) | 2024.11.08 |
| 【미분적분학 1】 Chapter 2. 함수의 변화율 (0) | 2024.11.07 |