
만약,

이면, 함수 f는 x=a에서 연속(continuous)한다.
함수의 연속은 '세 가지 조건'을 포함한다.

"함수 f는 임의의 점 x=a에서 연속이다."라는 명제의 필요충분조건은 위와 같은데, 즉 x=a에서 f의 극한은 존재하며 그 값은 f(a)가 된다.
자연의 많은 현상은 연속적이며, 연속함수로 해석할 수 있다. 예를 들어 물체의 움직임이나 개체 수의 변화는 시간에 따라 연속적으로 변한다.
- 연속적인 점에서 함수 값은 극한 값과 일치한다.
EXAMPLE. 함수의 불연속성

[그림 1] 함수의 그래프를 보고, a, b, 그리고 c 지점의 연속성에 대해 설명하시오.
SOLUTION.
[1] x=a에서 f(a)가 정의되지 않는다. ⇒ 불연속
[2] x=b에서 f(a)는 색칠된 점으로 정의된다. 그러나 lim_{x→b}[f(x)]는 정의되지 않는다. 왜냐하면 좌극한과 우극한이 서로 다르기 때문이다.
(1) 좌극한: 검은 점
(2) 우극한: 흰 점
⇒ 따라서 불연속하는 것으로 해석된다.

[3] x=c에서 좌극한과 우극한은 서로 같다. ⇒ (흰 점)
그러나 f(c)는 (검은 점)으로 함수의 연속 정의의 세 번째 조건(lim_{x→a} [f(x)]=f(a))을 만족하지 못한다.
⇒ 불연속

■
연속하는 함수의 세 가지 조건

■
반면 [그림 2]와 같은 그래프는 지점 a에서 '불연속적(discontinuous)'인데, 불연속 함수의 예제는 아래와 같다.

세 가지 그래프는 모두 discontinuous functions(특정 지점 a에 끊긴 함수)을 보여준다.
- [그림 2]의 첫 번째 그림: f(a)가 정의되지 않았다.
- [그림 2]의 두 번째 그림: f(a)는 검은 점으로 정의되었다. 그러나 좌극한과 우극한이 달라 limf(x)가 존재하지 않는다.
- [그림 2]의 세 번째 그림: f(a)는 검은 점이고, lim_{x→a}[f(x)]는 흰 점이다.
lim_{x→a}[f(x)] ≠ f(a)
함수의 연속성은 (1)방향 연속성과 (2)구간 연속성의 특성 또한 갖는다.
방향 연속성
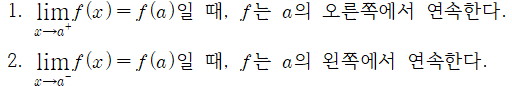
■
구간 연속성
함수 f가 어떠한 구간의 모든 점에서 연속할 때, f는 그 구간에서 또한 연속이다.
■
연속하는 함수는 다음과 같다.
1. 다항식(polynomials)
2. 유리함수(rational function)
3. 제곱근 함수
4. 삼각함수
5. 역삼각함수
6. 지수-로그 함수
불연속점 | Point of Discontinuity
미적분학에서 대표적인 불연속점(point of discontinuity)은 크게 3가지이며, 그래프(모습)는 다음과 같다.
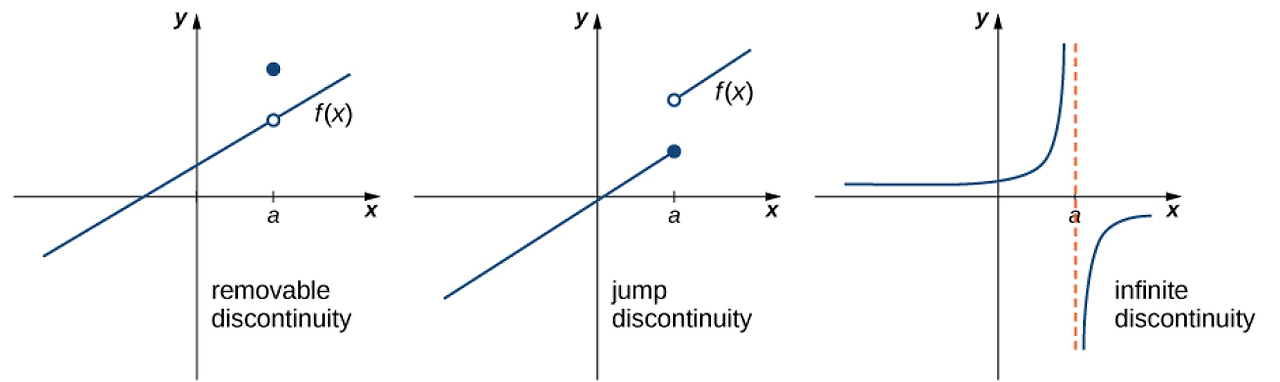
- 제거 가능 불연속점(removable discontinuity): 좌극한과 우극한이 서로 일치하나 f(a)의 값은 극한 값과 다르다.
- 비약 불연속점(jump discontinuity): 좌극한과 우극한이 서로 일치하지 않는다.
- 무한 불연속점(infinite discontinuity): 좌극한과 우극한의 불연속점이 무한대를 향한다.
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 8. 적용: 극한의 성질 (1) | 2024.11.13 |
|---|---|
| 【미분적분학 1】 Chapter 7. 극한의 성질 (0) | 2024.11.12 |
| 【미분적분학 1】 Chapter 5. 극한값의 필요충분조건 (0) | 2024.11.10 |
| 【미분적분학 1】 Chapter 4. 도함수 찾기 (0) | 2024.11.09 |
| 【미분적분학 1】 Chapter 3. 극한과 구간축소법 (0) | 2024.11.08 |