Herald-Lab
【미분적분학 1】 Chapter 2. 함수의 변화율 본문

앞선 챕터에서 우리는 미분적분학에서 핵심적으로 다루는 (1)함수와 (2)접선의 의미를 아래와 같이 공부하였다.
- 함수: 집합 X의 각 원소 x를 집합 Y에 있는 오직 한 원소 f(x)에 대응시키는 일련의 규칙, 원소 x는 독립변수, 함수값 또는 상 f(x)는 종속변수이다.
- 접선: 어떠한 그래프 상에 '한 지점에 접하는 직선', 할선의 기울기의 극한으로 값을 구한다.
미분에 대한 접근
Approach to Differentiation
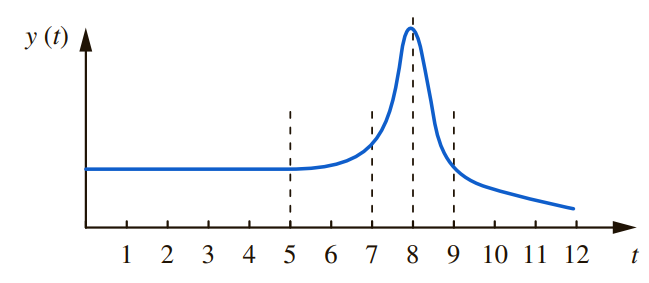
[그림 1]을 통해 주어진 함수는 다음과 같이 변화함을 알 수 있다.
- 0~5초: 변화율 없음
- 5~7초: 우상향 변화, y의 변화율은 양의 값을 가짐
- 7~8초: 우상향 변화, 5~7초보다 더욱 급변함
- 8~9초: 우하향 변화, y의 변화율은 음의 값을 가짐
- 9~12초: 우하향 변화, 8~9초보다 완만하게 변화함
미분적분학에서 미분학(differential calculus)은 함수의 변화율을 명확히 기술하는 것이 그 목표이다.
- 함수의 변화율에 대한 정확한 표현 또는 식을 구하는 과정을 미분(differentiation)이라고 한다.
참고로 미분이라 번역되는 단어는 실제 영문에서 아래와 같이 번역된다.

함수의 변화율
Rate of Change of a Function
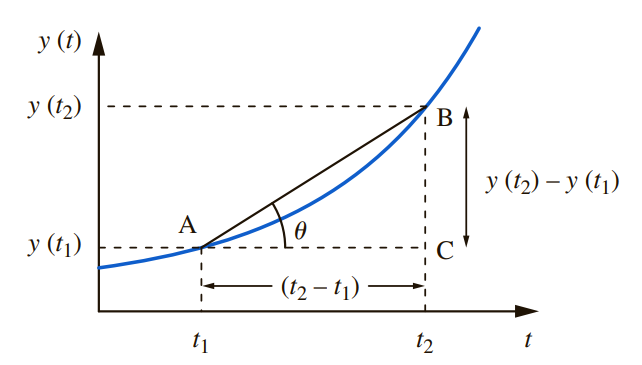
[그림 2]의 A와 B는 각각 t=t_1일 때 함수 y(t_1)의 값, t=t_2일 때 함수 y(t_2)의 값을 나타낸다.
- 구간 t_1에서 t_2 사이의 y의 변화량은 다음과 같다.
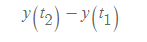
- 함수의 변화량은 구간 사이의 변화량 분의 y의 변화량이다.
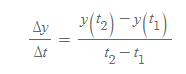
여기서 델타 Δ는 나중 값 - 처음(기준) 값을 나타낸다.
[그림 2]에서 A와 B를 연결한 직선을 현(chord)이라 하고 그래프 상에서는 이 chord의 기울어짐을 평균 변화율이라 한다.
- 함수의 변화량 식을 응용하면 chord의 기울어짐은 아래와 같이 정의할 수 있다.
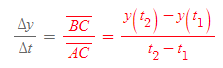
그래프 상의 chord의 기울어짐은 일반적인 함수의 기울기(그래디언트, slope)와 같다.
- 두 점 사이의 함수의 평균 변화율은 현의 기울어짐이자 함수의 기울기와 같다.
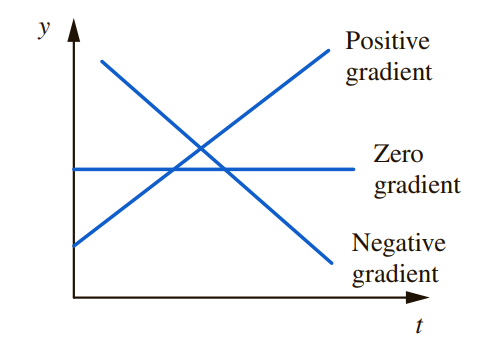
[그림 3]은 t축을 따라 기울기를 (1)양의 기울기, (2)0의 기울기, (3)음의 기울기로 각각 분류한 것이다.
임의의 점에서의 함수 변화율
Rate Change of a Function at a Specific Point
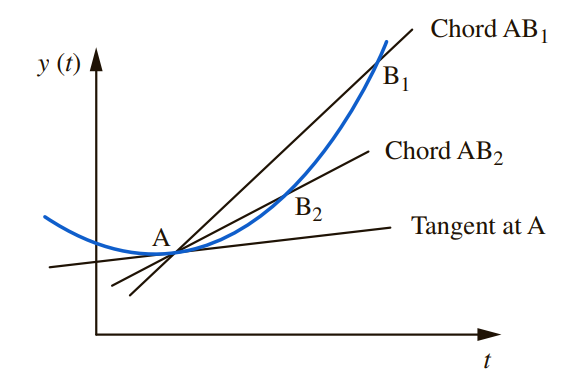
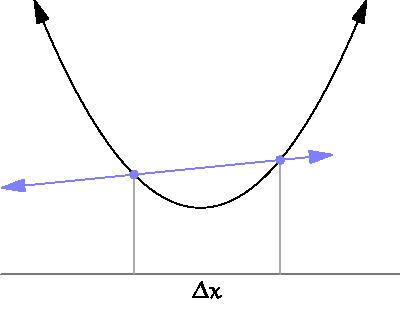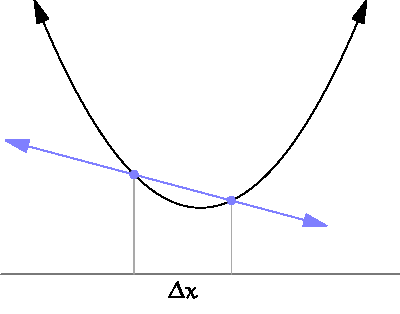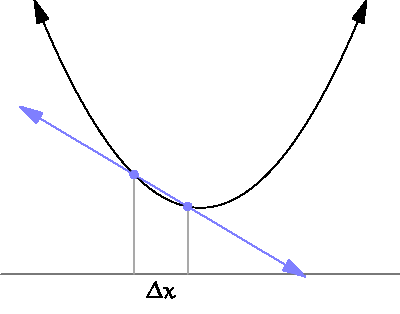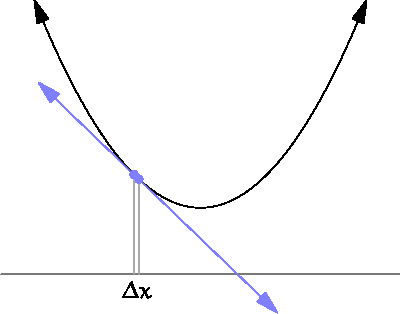
특정한 지점에서의 함수 변화율을 알고 싶다면 (1)구간 Δt를 줄임으로써 (2)결과적으로 B를 A와 가깝게 배치해 (3)A와 최대한 근접한 구간의 기울기를 구함으로써 함수 변화율의 근사값을 구할 수 있다.
- [그림 4]의 chord AB는 B1에서 B2로 옮겨짐에 따라 점 A에서의 접선과 근사한다.
- 곡선 상의 점 A에서의 함수 변화율은, chord를 점 A에 근사함에 따라 결국 접선의 기울기와 같아진다.
- 접선(tangent): 곡선과 직선이 서로 한 점에서 만날 때, 이때의 직선을 '곡선에 대한 접선'이라고 한다.
어떤 곡선 상의 점 A에서 함수의 변화율이란, 접선의 기울기이다.
많은 과학분야에서 실제 유효한 함수는 하나의 입력에 대해 오직 하나의 출력만을 발생시키는 것이다. 그리고 이러한 원소(x)-함수값(f(x)) 관계는 평면 상에 2차원의 그래프로 나타나는데, 그 중 특정한 지점(접점)에서 기울기가 바로 함수의 변화율이다.
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 4. 도함수 찾기 (0) | 2024.11.09 |
|---|---|
| 【미분적분학 1】 Chapter 3. 극한과 구간축소법 (0) | 2024.11.08 |
| 【미분적분학 1】 Chapter 1. 함수와 접선 (0) | 2024.11.06 |
| [대학수학 - 미분적분학] 10. 삼각함수의 극한과 무한소 (0) | 2023.08.31 |
| [대학수학 - 미분적분학] 09. 지수함수의 도함수 (0) | 2023.08.24 |





