[물리학-고전역학] 중력장 운동 - 포물체 운동 | Projectile Motion

 

그림 1. 일상에서의 포물선 궤도

 

 

포물체 운동(projectile motion): 지표면을 경계로 비스듬히 위로 던진 물체[그림 2]의 운동으로 포물선(포물궤도, trajectory)[그림 1]을 이루는 것이 특징이다.

 

그림 2. 포물궤도 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.99]

 

 

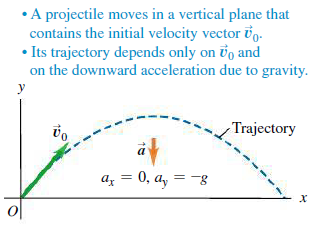
• 공기의 저항을 무시한다면 마찬가지로 중력에 의해서만 영향을 받는 독특한 운동이다.
• 포물선은 2차원의 평면에 나타나는 기하학적 모양이므로, 성분 또한 x축과 y축으로 나뉠 수 있다.
• 수평방향: 등속도 운동
• 수직방향: 연직상방 운동

​

[고전역학_중력장 운동 - 연직상방운동, 연직하방운동]에서 배운 연직상방운동의 운동학 식을 사용할 것이다.

 

[물리학-고전역학] 중력장 운동 - 연직상방운동, 연직하방운동 | Vertical Upward, Vertical Downward Motion

 

포물체 운동의 분석

포물체 운동을 분석함에 있어 아래 다섯 가지 요소[그림 3]는 반드시 집고 넘어가야 한다.

1. 초속도 v_i
2. 가속도 a
3. 힘 F
4. 최고점 도달시 t
5. 거리: 최고높이(y-) h와 최대수평도달거리(x-) R

 

그림 3. 포물체가 가진 물리량 [출처: Principles of Physics, Serway & Jewett, 12th ed., 2012, p.76]

 

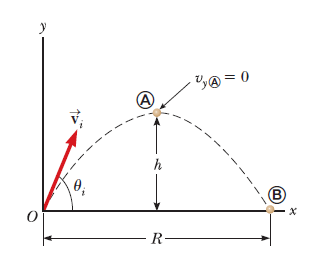
포물체 운동 가정

• 자유낙하 가속도(중력가속도)는 높이와 관계없이 항상 일정하고 방향은 아래를 향한다.
• 공기저항을 무시한다. cf. 포물선을 그리는 물체가 매우 빠른 속력으로 이동한다면 공기의 유체저항도 고려해야 한다. ⇒ 인공위성의 예측 궤도 계산에 주요 어려움으로 작용

​

포물체 운동 분석

1. 수평방향

 

 

2. 수직방향

​

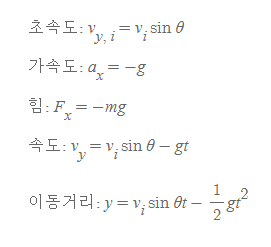
포물체 운동을 하는 물체의 최대수평도달거리와 최대 연직 높이

t_i =0일 때, 포물체를 v_y, i 성분 방향으로 쏘아 올리는 상황을 떠올려 보자.

• 만약 포물체가 t시간이 지난 이후 최고점 h에 도달한다면, 이후 방해 요소가 없는 한은 포물체를 처음 쏘아올린 수평면 높이로 되돌아오는 데 정확히 2t만큼의 시간이 걸린다.
• 포물체의 운동에서 특별히 관심을 두는 위치는 다음과 같다.

1. 최고점: 포물체가 가지는 최대 연직방향위치로 좌표는 (R/2, h)이다.
2. 최종점: 포물체가 가지는 최대 수평방향위치로 좌표는 (R, h=0)이다.

• 포물체 운동에서의 물리량과 그 특징

1. 최대수평도달거리 R: 포물체가 수평방향으로 나가간 최대거리로 그 크기는 기호 R로 표현한다.
2. 최대높이 h: 포물체가 연직방향으로 올라간 최대높이로 최고점에서는 v_y = 0을 만족한다. 따라서 아래와 같은 식을 세울 수 있다.

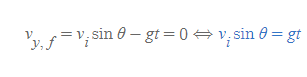
3. 최대높이(최고점) 도달시(time at which the projectile reaches peaks): 포물체가 최대높이에 도달하는 데 걸린 시간으로 최대높이의 수식 조건으로부터 쉽게 유도할 수 있다.

​

최대높이 도달시

■

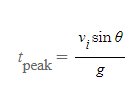
최대 높이

최대높이 도달시를 대입해 최대높이를 계산할 수 있다.

​​

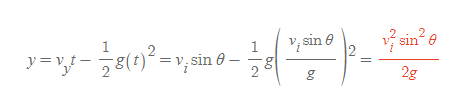
q.e.d.

최대높이

■

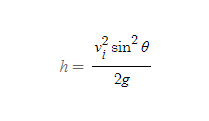
최대수평도달거리

[1] 포물체가 수평도달거리에 도달하기 위해선 최대높이 도달시의 2배가 되는 시간이 필요하다.

 

 

[2] 포물체의 수평도달거리는 성분을 이용하고 식을 활용한다.

​​

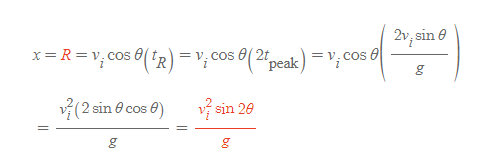
q.e.d.

최대수평도달거리

 

■

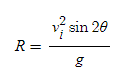
• sin값은 90도일 때 1이라는 최댓값을 가지기 때문에, 포물체가 45도로 발사되었을 때 최대수평도달거리에 도달한다.

​

위의 두 가지 공식(최대높이, 최대수평도달거리)은 최대높이 도달시를 적용한다는 전제 하에 (1)x축에 대한 등속도 운동 v-t 그래프와 (2)y축에 대한 연직상방운동을 그림으로써 기하학적으로도 쉽게 유도할 수 있다.

• x축의 t에 최대높이 도달시의 식을 대입한다.

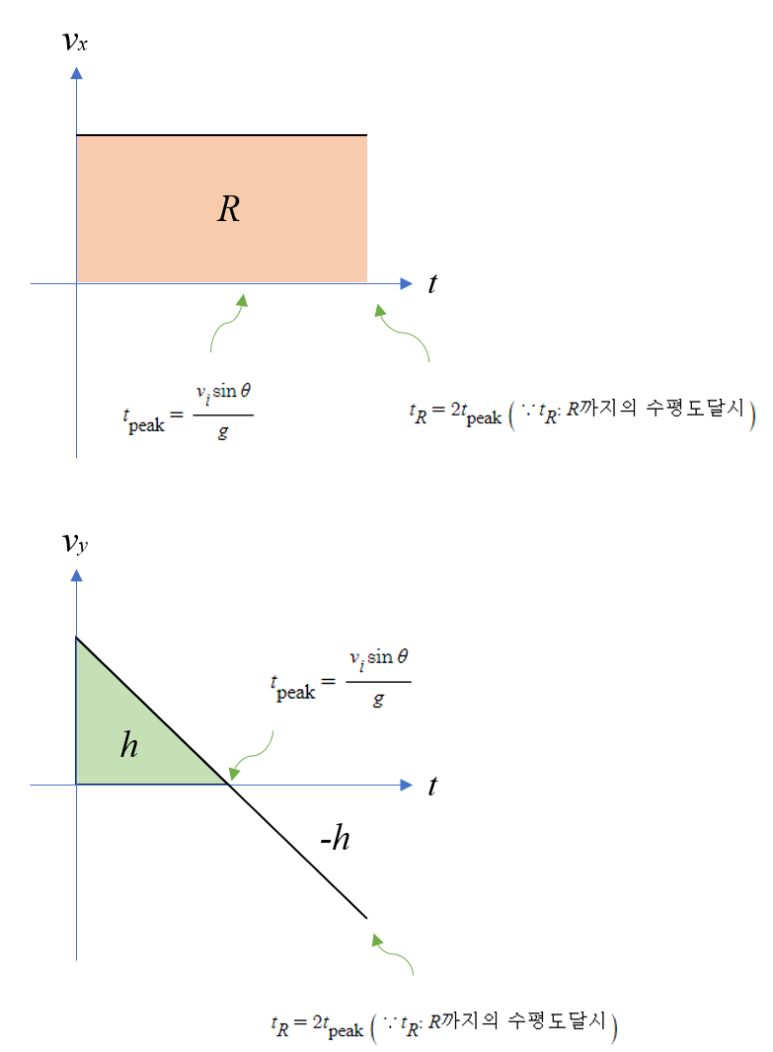
그림 4. 최대수평도달거리 R과 최대높이 h의 기하학적 모형: v-t 그래프를 활용하였다.

​