728x90
반응형

이번 챕터에서 소개할 토크의 두 번째 식을 파악하기 위해 [고전역학_43. 토크 1]과 [고전역학_44. 회전운동에너지와 관성모멘트]를 우선 복습하도록 한다.
[물리학-고전역학] 43. 토크 1 | Torque (1)
토크(돌림힘, 회전력) 토크(돌림힘, 회전력, torque): 회전축이 있는 강체의 특정 지점에 힘을 가하면 물체...
blog.naver.com
알짜 토크가 주어진 강체
접선 방향의 알짜힘 벡터 F_t와 지름 방향의 알짜힘 벡터 F_r에 의해 반지름 r인 원 주위를 회전하는 질량 m의 입자를 떠올려 보자.
- 접선방향의 힘은 접선 가속도 a_t를 만들어낸다.
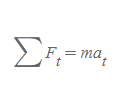
- 원의 중심을 통과하고 지면에 수직인 축에 대해 알짜토크의 크기는 다음과 같다.
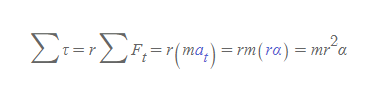
위의 식에서 mr^2은 관성모멘트 I와 같다.
- 입자에 작용한 알짜 토크는 각가속도 α에 비례하고, 비례상수는 관성모멘트 I이다.
- 뉴턴의 운동 제2법칙인 가속도의 법칙과 수학적으로 같은 형태이다.
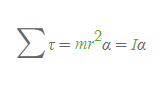
위와 같은 논리를 임의의 모양을 한 강체로 확장하면 아주 작은 크기의 질량 요소 dm이 무한히 많이 모인 것으로 간주할 수 있다.
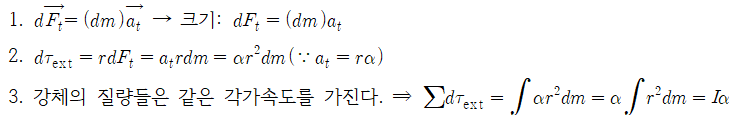
알짜힘 토크 | Torque by Net Forces
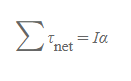
■
- 의미: 토크는 강체의 관성모멘트와 각가속도에 비례한다.
- 관성모멘트는 강체의 크기, 모양에 따라 값이 결정된다.
- 지름성분이 축에 대해 만들어내는 토크는 0이다.
회전운동에서 일과 회전운동에너지
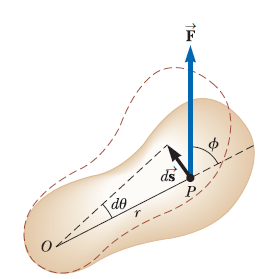
[그림 1]과 같이 회전축 O에 대해 회전하는 강체에 단일외력 F가 점 P에 작용하고, ds만큼 움직였을 때, 외력 F가 강체에 한 미소 일은 다음과 같다.
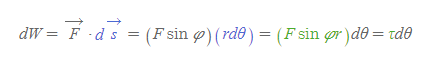
시간 dt동안 고정축에 대해 물체가 dθ만큼 움직일 때 외력이 한 순간 일률은 아래와 같다.
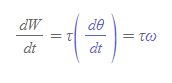
회전운동에서 일-회전운동에너지 정리 | Work-Kinetic Energy Theorem for Pure Rotation
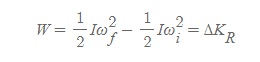
■
[고전역학_21. 일과 에너지]에서 배운 일-운동에너지 정리 내용을 떠올리면 위의 식이 어떻게 나왔는 지 쉽게 이해할 수 있다.
- 어떤 계에 일이 가해지고 이 system의 유일한 변화가 속력뿐이라면, 알짜힘이 계에 한 일은 곧 계의 운동에너지 변화이다.
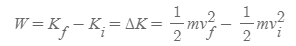
728x90
반응형
'고급물리학 > 고전역학' 카테고리의 다른 글
| [물리학-고전역학] 48. 벡터 미적분학: 다이버전스(발산) | Divergence (0) | 2024.01.01 |
|---|---|
| [물리학-고전역학] 47. 벡터 미적분학: 그래디언트(기울기) | Gradient (0) | 2023.12.30 |
| [물리학-고전역학] 45. 물리학 고전읽기: 칸트의 물리적 모나드론(1756) | Monadologia Physica (0) | 2023.12.14 |
| [물리학-고전역학] 44. 회전운동에너지와 관성모멘트 | Rotational Kinetic Energy and Moment of Inertia (1) | 2023.12.11 |
| [물리학-고전역학] 43. 토크 1 | Torque (1) (1) | 2023.12.10 |