[물리학-고전역학] 43. 토크 1 | Torque (1)

 

토크(돌림힘, 회전력)

Torque

 

토크(돌림힘, 회전력, torque): 회전축이 있는 강체의 특정 지점에 힘을 가하면 물체는 회전축에 대해 회전운동을 하려하는 데 이때 회전에 대해 '토크가 걸리다'라고 표현한다.

• 토크가 걸릴 때, 힘의 작용선 상에 있지 않은 어떤 평면 상의 한 점에서 회전력을 유발하는 효과를 보인다.
• 돌림힘은 토크와 같이 자주 쓰이는 용어로 어떤 축에 대해 물체를 회전시키고자 하는 힘 그 자체를 나타낸다.
• 토크는 벡터량이다.

 

그림 1. 토크에 의한 물체의 돌림 도식

 

 

토크를 기술할 때, [그림 1]과 같이 돌림힘이 작용하는 지점과 회전축, 그리고 힘의 작용선(line of action)과 수직을 이루는 거리 d인 모멘트 팔(moment arm)[그림 2]을 정의할 수 있다.

 

그림 2. 토크의 물리량

 

​

토크 크기 | Magnitude of Torque

 

■

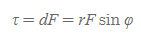
• 물리량

1. r: 회전축 O와 힘의 작용점 사이의 거리
2. F: 힘의 작용점에 준 힘의 크기
3. φ: 벡터 r과 벡터 F 사이의 최소각도 ⇒ 벡터 r은 회전축에서 힘의 작용점으로 향하는 최단거리를 갖는 방향벡터이고, 벡터 F는 작용점에 준 힘이다.
4. d: 모멘트 팔, 회전축에서 힘의 작용선 방향으로 수선을 그엇을 때, 회전축에서 만나는 지점까지의 길이

​

특히 r의 길이와 모멘트 팔 d를 잘 구분하도록 한다. r은 물체의 회전축 O에서부터 힘이 작용한 지점까지의 거리이고, d는 회전축에서 힘의 작용선 방향으로 수선을 그었을 때, 힘의 작용선에 도달한 순간, 회전축에서부터의 길이다.

​

토크 크기에서 우리는 방향벡터 r, 힘 벡터 F, 그리고 이 두 벡터 사이의 최소각 φ가 포함된 sinφ가 항으로 들어감을 알 수 있었다. 이들 항은 모두 벡터곱으로도 표현가능한 내용으로 결국 토크 또한 벡터곱으로 정의할 수 있다.

​

토크 | Torque

■

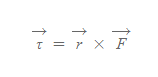
• 의미: 토크를 cross product로 정의할 수 있으며, 계산 결과 토크 물리량 자체도 역시 벡터량이다.

 

그림 3. 벡터곱의 방향

 

 

• 토크의 방향은 [그림 4]와 같이 벡터곱의 방향[그림 3]과 일치한다.

 

그림 4. 토크의 방향

 

​

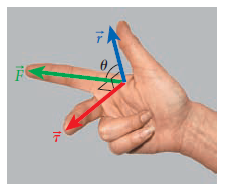
토크의 특징

• 강체를 회전하게 하는 F의 성분은 Fsinφ이다. ⇒ 회전축과 힘의 작용점에 이르는 직선에 대한 수직성분
• 회전의 모멘트는 F와 d에 비례한다.
• 토크의 방향: 토크는 벡터 r와 벡터 F가 놓인 평면에 대해 수직한 z-축으로 방향성[그림 5]을 갖는다.
• 토크의 부호: z-축 반시계 방향 (+), 시계 방향 (-) ⇒ 물체의 회전 방향에 따라 토크의 부호를 정할 수 있다.

 

그림 5. 토크의 방향성

 

​

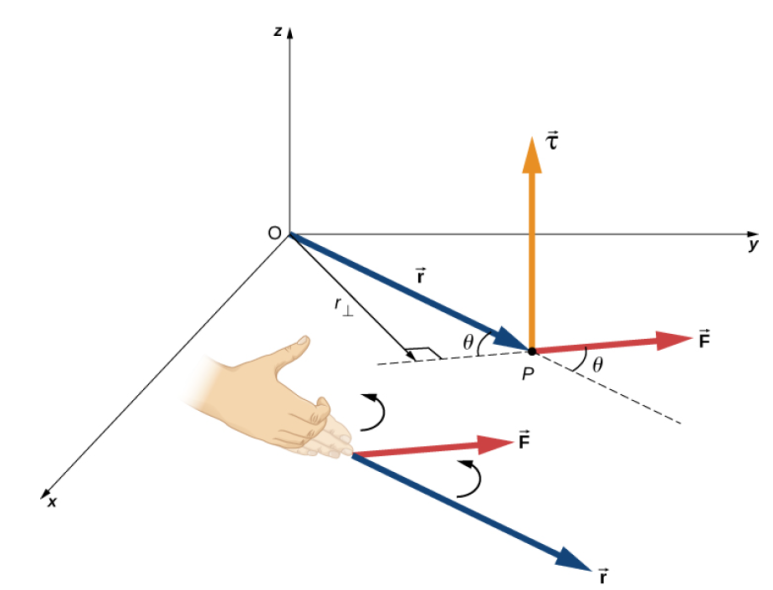
토크에 따른 운동의 형태

1. 토크가 일정할 때, 등각가속도 운동을 한다.
2. 토크가 변화하면, 각가속도가 변하는 운동을 한다.
3. 토크가 0일 때, (1)회전하고 있는 물체는 등속 원운동을 지속적으로 하고, (2)회전이 멈춘 물체는 더 이상 회전하지 않는다.