[물리학-고전역학] 41. 회전 운동 | Rotation Around a Fixed Axis

 

회전 운동

Rotational Motion

 

회전: 한 점으로 대표되는 축을 중심으로 하여 어떤 물체가 빙빙 도는 것

• 축은 회전에서 중심 O(원점, origin)로 표현되며, 물체는 일반적으로 강체를 들 수 있다. 그러나 [그림 1]과 같이 공기 분자 집합(air mass)이 만드는 허리케인 또한 회전 운동으로 간주된다.

 

그림 1. 허리케인

 

• 강체(rigid body): 힘이 가해졌을 때 변형되지 않는 물체, 강체를 이루는 입자들 간의 상대 위치는 항상 일정하다.

​

회전축을 주위로 하는 회전운동은 종종 아래와 같이 분류된다.

1. 강체 고정축 회전운동: 평면 상에서 고정축을 중심으로 한 강체의 회전 운동[그림 2] e.g. 팽이
2. 강체 굴림운동(rolling motion): 평면 상에서 고정축 없이 병진 운동과 회전 운동이 함께 나타나는 운동

 

그림 2. 강체 고정축 회전운동

 

 

 

각도, 각속도, 그리고 각가속도

Angle, Angular Velocity, and Angular Acceleration

 

각도설정

회전하는 운동을 설명할 때는 극좌표(polar coordinate)를 사용한다. ⇒ 회전하는 '물체의 조각입자'의 위치[그림 3]는 (r, θ)로 표기한다.

 

그림 3. 회전운동의 위치 물리량

 

 

• r: 회전축인 원점으로부터 떨어진 거리
• θ: 물체가 회전할 때 돌아간 정도로 기준선에서 반시계 방향으로 측정한다.

1. 반시계 방향이 (+) 부호를 갖는다.
2. 시계 방향은 (-) 부호를 갖는다.

​

그리고 회전 운동을 통해 그려진 호의 길이를 s라 하고, 각도의 n도(degrees) 대신 라디안(radian)으로 정의하여, 1 라디안을 다음과 같이 정의[그림 4]한다.

​

원호와 각도

■

• 각도는 단위가 없는 수(pure number)이나, 회전 운동에서는 의미있는 단위인 [rad]를 붙여준다.

​

1 라디안

■

 

그림 4. 1[rad]와 원호-각도의 정의 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.298]

 

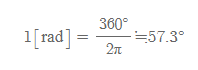
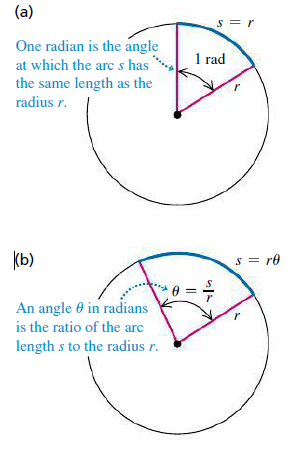
1 [rad]는 호의 길이와 호의 반지름이 정확하게 일치할 때의 각도를 의미한다.

• 라디안은 실수(real number) 표현 혹은 (pi)와 같은 특정 상수와 함께 쓴다. cf. n도(degree) 기호와 함께 쓰지 않는다.
• π란, 원둘레(circumference) C / 지름(diameter) d의 값이다.

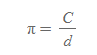
각위치, 각변위, 각속도, 각가속도

각위치(angular position): 회전하는 전체강체가 가지는 각도

각변위(angular displacement)[그림 5]

 

그림 5. 각변위

 

 

각변위는 xy-평면을 두고 x-축을 기준으로 물체가 회전하는 각 θ를 이용한다.

1. 양의 x-축으로부터 반시계 방향으로 측정한 각을 양수로 선택한다.
2. 양의 x-축으로부터 시계 방향으로 측정한 각은 음수로 취급한다.

​

[그림 5]는 x-축으로부터 반시계 방향으로 돌았으므로 각변위는 양수 값을 갖는다.

​

각속도(angular velocity): 강체의 각변위를 그 변위가 일어난 시간 간격 Δt로 나눈 비율, 강체의 회전운동은 시간에 대한 θ의 변화율로 기술할 수 있다.

​

평균 각속도 | Average Angular Velocity

■

​

​

순간 각속도 | Instantaneous Angular Velocity [그림 6]

■

순간 각속도는 시간간격이 0으로 접근할 때, 평균 각속도의 극한 값이다.

 

그림 6. 각속도

 

 

• 각속도는 일반적으로 순간 각속도를 의미한다.
• 각속도의 단위: [rad/s]
• 부호: 강체가 반시계 방향으로 돌 때 각변위는 양수이고, 따라서 각속도도 양의 부호를 가진다.
• 각속력: 각속도의 크기, 음수가 될 수 없다.

​

주어진 시간 동안 회전하는 강체의 여러 점들은 그 점의 회전축으로부터 떨어진 거리에 따라 각각 다른 거리를 움직인다. 그러나 어느 순간에서나 회전하는 강체의 모든 부분은 같은 각속도를 가진다.

​

벡터량으로서 각속도와 각가속도의 방향은 '순간(instantaneous)'의 조건에서만 유의미하다.

• 유한한 회전의 경우 각 변위를 벡터합으로 연산 할 수 없다.
• 벡터 각속도의 방향은 벡터곱을 정의할 때 사용한 오른손 법칙(오른손 규칙, right-hand rule)[그림 7]으로 주어진다. ⇒ 회전시켰을 때 엄지가 지면을 뚫고 나오면 각속도는 (+)방향성을 가졌다고 본다.

 

그림 7. 오른손 법칙

 

 

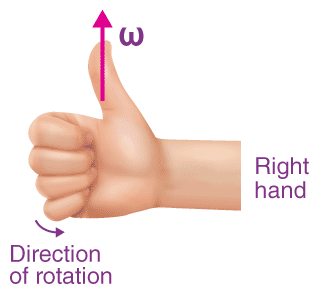
강체가 각가속도를 가질 때 강체의 각속도가 변한다.

​

평균 각가속도 | Average Angular Acceleration

■

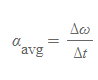
• 의미: 각속도의 변화에 시간 간격을 나눈 값

​

순간 각가속도 | Instantaneous Angular Acceleration

■

• 의미: 시간간격이 0에 접근할 때 평균 각가속도의 극한
• 각가속도는 일반적으로 순간 각가속도를 의미한다.
• 단위: [rad/s^2]
• 양의 부호를 가지는 조건

1. 반시계 방향으로 회전하는 강체가 빨라지는 경우
2. 시계방향으로 회전하는 강체가 느려지는 경우

​

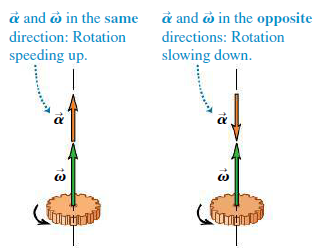
벡터 각가속도의 특징[그림 8]

1. 각가속도와 각속도의 방향이 서로 같다. ⇒ 강체의 회전이 빨라진다.
2. 각가속도와 각속도의 방향이 서로 다르다. ⇒ 강체의 회전이 느려진다.

 

그림 8. 회전의 속력 변화: 각가속도 α와 각속도 ω의 방향이 서로 같을 때, 회전 속력은 빨라진다(rotation speeding up).

 

​