반응형
250x250
Notice
Recent Posts
Recent Comments
Link
Herald-Lab
【미분적분학 1】 Chapter 12. 미분법: 새로운 도함수 구하기 본문
728x90
반응형

새로운 함수가 이전의 함수들을 더하거나 빼거나, 또는 상수배하여 만들어진 것이라면, 그 도함수는 이전의 함수의 도함수에 의해 계산된다.
상수배 법칙 | Constant Multiple Rule

■
g(x)=cf(x)라 하자.

합 법칙 | Sum Rule

■
F(x)=f(x)+g(x)라 하자.
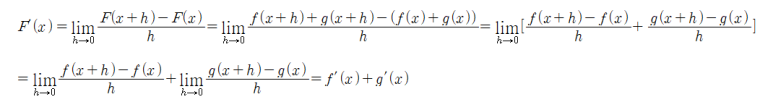
차 법칙 | Difference Rule

■
차 법칙 역시 합 법칙과 마찬가지로 부호만 바꾸면 같은 방식으로 증명이 가능하다.
EXAMPLE. 상수배, 합, 차
아래 주어진 함수에 대한 도함수를 각각 구하시오. (7문항)
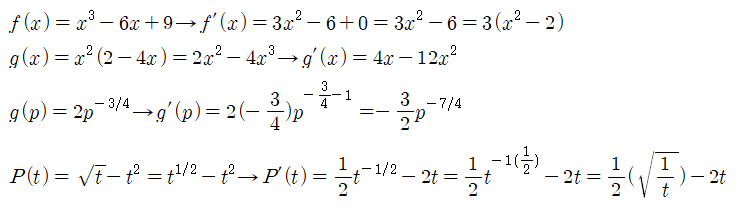
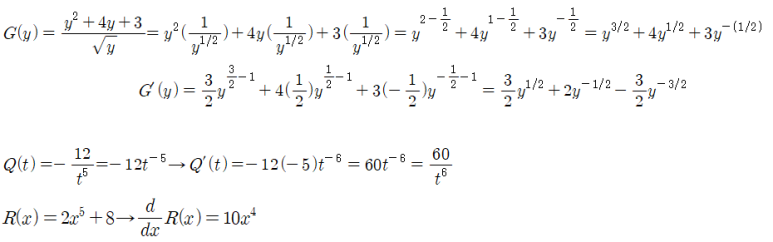
■
물체의 움직임
Motion of an Object
n차 도함수는 n-1차 도함수의 변화율과 같으며, 이는 물리학에서 물체의 움직임을 설명하는 운동학과 밀접하다. 위치가 시간의 함수일 때, 속도는 위치함수 s(t)의 도함수이다. 또한 가속도는 속도함수 v(t)의 도함수이다.
속도함수

■
가속도함수

■
EXAMPLE. 순간속도
시간에 대해 s(t)=4.9t^2[m]만큼 움직이는 물체의 t=5[초]에서의 순간속도를 구하시오.
SOLUTION.
위치함수의 도함수인 v(t)를 통해 물체의 순간속도를 쉽게 구할 수 있다.
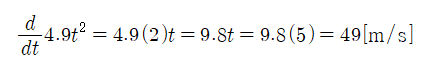
■
728x90
반응형
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 14. 극한부정형과 로피탈 정리 (0) | 2024.11.25 |
|---|---|
| 【미분적분학 1】 Chapter 13. 자연로그 밑 e (0) | 2024.11.24 |
| 【미분적분학 1】 Chapter 11. 미분법: 다항함수 도함수 (0) | 2024.11.16 |
| 【미분적분학 1】 Chapter 10. 엡실론-델타 논법 (0) | 2024.11.15 |
| 【미분적분학 1】 Chapter 9. 삼각함수와 극한 (2) | 2024.11.14 |





