Herald-Lab
【미분적분학 1】 Chapter 11. 미분법: 다항함수 도함수 본문

[Chapter 4. 도함수 찾기]에서 배운 미분계수의 개념에서 a(점 P의 x값)는 고정된 수였다. 그러나 지금부터는 이 a를 변할 수 있는 값으로 생각한다. 미분계수의 식에 a를 변수 x로 바꾸면, 도함수가 정의된다.
도함수 | Derivative
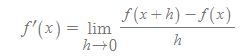
■
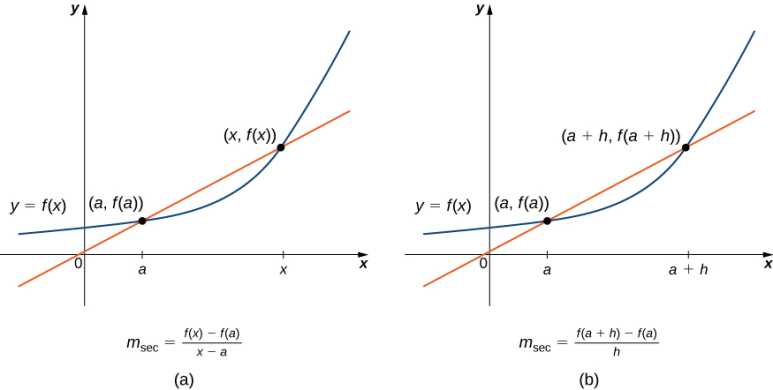
- 의미: x에서의 f'(x)의 값은 기하학적으로 점 (x, f'(x))에서 f의 그래프에 접하는 접선의 기울기[그림 1]이다.
- f'(x)는 f의 도함수(derivative of f)로 정의된다.
- f'(x)의 정의역은 {x | ∃f'(x)}이며, 이 값은 f의 정의역보다 크지 않다.
EXAMPLE. 도함수
함수 f(x)가 아래와 같이 주어졌을 때, f'(x)를 구하시오.
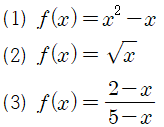
SOLUTION.
(1)
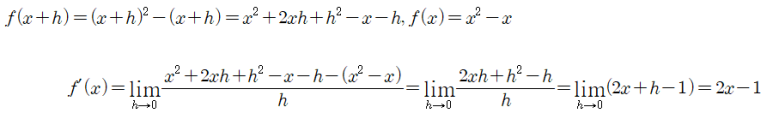
(2)
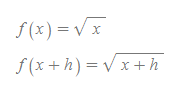
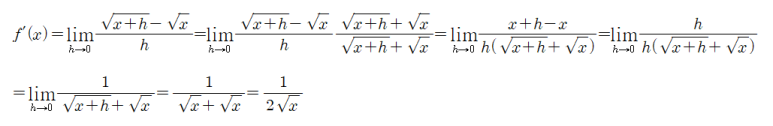
(3)
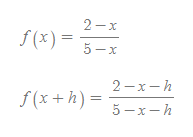
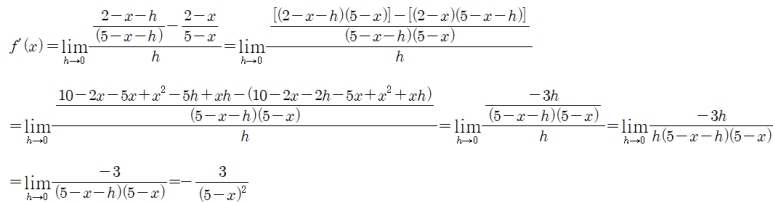
■
위의 계산식은 그 과정이 너무나 복잡한 데 앞으로 미분법을 학습함으로써 이러한 계산의 '패턴'을 학습하게 되고, 이를 이용해 식들을 매우 간단한 방식으로 풀 것이다.
다항함수의 도함수
Derivatives of Polynomials
상수함수
모든 함수 중 상수함수(constant function)는 가장 간단한 함수로 그래프[그림 2]는 아래와 같이 나타난다.
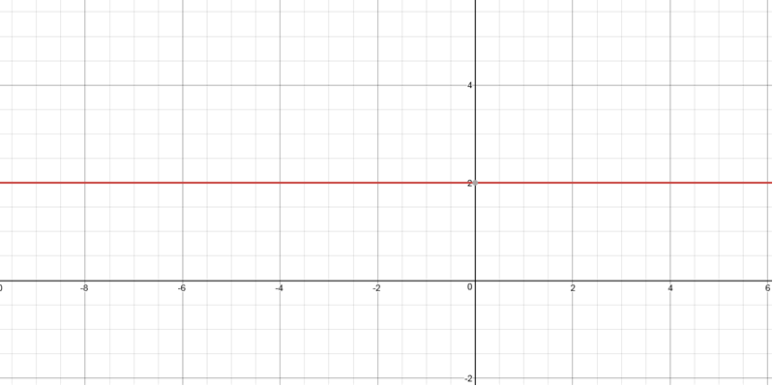
가장 간단한 형태인 상수함수 f(x)=c의 도함수는 아래 증명을 통해 다음과 같이 계산한다.
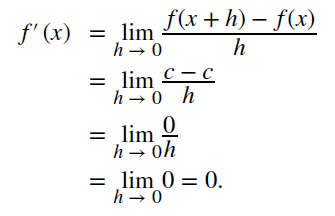
상수함수 도함수 | Constant Rule
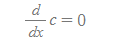
■
거듭제곱함수
n이 양의 정수일 때, 함수 f(x)=x^n을 거듭제곱함수라고 하고, 예를 들어 n=2라고 하자.
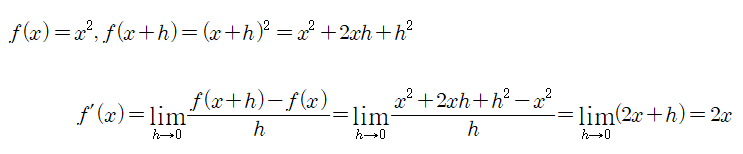
다음 n=3이라고 하자.
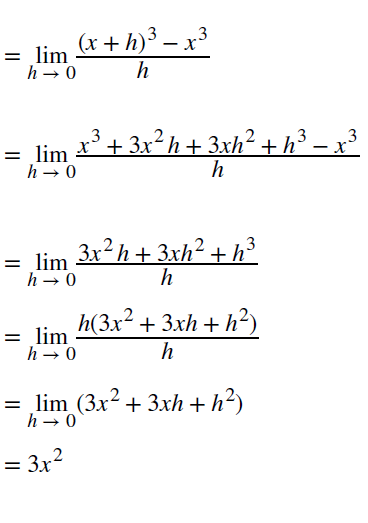
연산을 반복하면 어떠한 규칙성이 나타나는데, n이 양의 정수일 때, 양의 거듭제곱법칙(power rule)을 아래와 같이 정리할 수 있다.
양의 거듭제곱법칙 | Power Rule
n이 만약 양의 정수일 때,
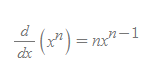
■
음의 정수를 지수로 갖는 거듭제곱함수의 도함수도 거듭제곱법칙이 성립한다.
거듭제곱법칙 | Power Rule
n을 임의의 실수(R)라 하면, 거듭제곱법칙의 일반형은 아래와 같다.
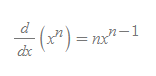
■
EXAMPLE. 거듭제곱법칙
다음 도함수를 거듭제곱법칙을 활용하여 구하시오.
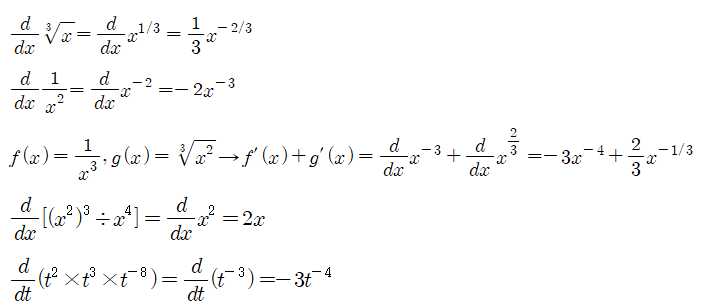
■
법선 방정식
거듭제곱법칙을 활용해 접선을 매우 쉽게 구할 수 있다. 또한 이 접선 정보를 활용해 법선(normal)[그림 3]까지 구할 수 있다.
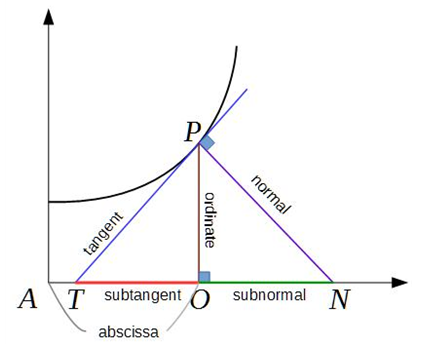
법선 방정식
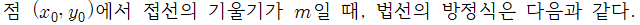
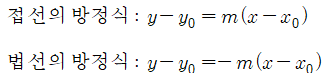
■
EXAMPLE. 법선 방정식

SOLUTION.
[1] 접선(m)의 방정식
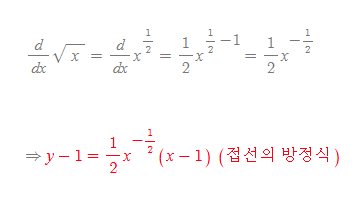
[2] 법선(-m)의 방정식

■
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 13. 자연로그 밑 e (0) | 2024.11.24 |
|---|---|
| 【미분적분학 1】 Chapter 12. 미분법: 새로운 도함수 구하기 (0) | 2024.11.19 |
| 【미분적분학 1】 Chapter 10. 엡실론-델타 논법 (0) | 2024.11.15 |
| 【미분적분학 1】 Chapter 9. 삼각함수와 극한 (2) | 2024.11.14 |
| 【미분적분학 1】 Chapter 8. 적용: 극한의 성질 (1) | 2024.11.13 |





