
삼각함수(trigonometric function): 각도와 관련된 여러가지 함수
- 삼각함수는 기본적으로 3가지 함수-sine 함수, cosine 함수, tangent 함수-가 있으며, 이들의 역수-cosecant, secant, cotangent-를 모두 합치면 총 6개이다.
삼각함수의 정의

삼각함수는 먼저 직각삼각형[그림 1]을 통해 다음과 같이 정의할 수 있다.

삼각함수의 직각삼각형 정의의 역수는 각각 코시컨트, 시컨트, 그리고 코탄젠트의 정의와 같다.
또한 단위원(unit circle: 반지름 r이 1인 원으로 원점 (0, 0)을 중심으로 한다.)으로 삼각함수를 정의할 수도 있다.

반지름을 r이라 둘 때, 각 삼각함수의 정의는 다음과 같이 정리한다.
1. sinθ = y/r
2. cosθ = x/r
3. tanθ = y/x = sinθ/cosθ
4. secθ = 1/cosθ
5. cscθ = 1/sinθ
6. cotθ = 1/tanθ = cosθ/sinθ
sine 그래프와 cosine 그래프[그림 3], 그리고 tangent 그래프는 아래[그림 4]와 같이 그릴 수 있다.


삼각함수의 성질
삼각함수는 다양한 정의만큼 여러가지 성질을 가지고 있는데, 자주 사용하는 삼각함수의 성질을 다음과 같이 정리할 수 있다.
1. 주기성: 삼각함수의 그래프를 통해 이들이 2π(sine, cosine) 혹은 π(tangent)의 주기(period)를 가짐을 알수 있다.
2. 특수각에서의 삼각함수의 값

3. 항등식(trigonometric identity): 삼각함수가 나오는 항등식으로 복잡한 삼각함수 식을 간단히 정리하는 데 유용하다.
(1) 피타고라스 정리
삼각함수의 피타고라스 정리
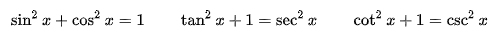
■
- 여기서 sin^2(x)는 (sinx)^2과 같다.
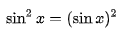
(2) 삼각함수의 덧셈정리
두 삼각함수를 연결하는 연산자의 종류에 따라 2가지 항등식을 가지며, 이들은 삼각함수의 가법으로 쉽게 유도할 수 있다.
삼각함수의 가법
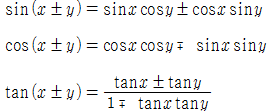
■
삼각함수의 합곱 변환식
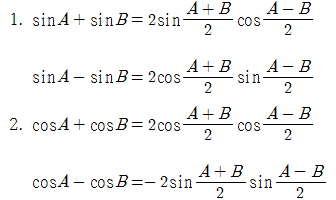
삼각함수의 곱합 변환식
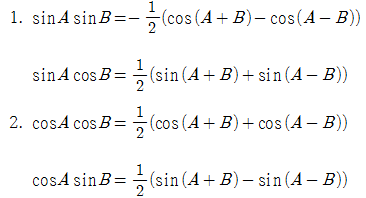
(3) 삼각함수의 배각공식(double-angle formula)
삼각함수의 가법으로 배각공식을 유도할 수도 있다.
배각공식
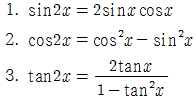
■
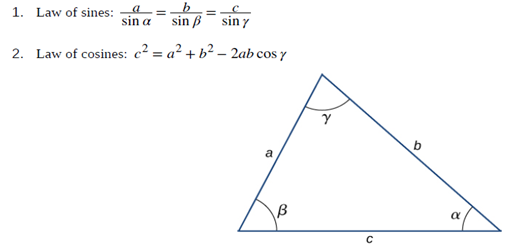
(4) 사인법칙과 코사인법칙
미분의 여러 가지 내용을 증명하는 데 삼각함수의 극한 값들이 중요하게 활용된다.
사인 함수
sinx의 극한
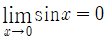
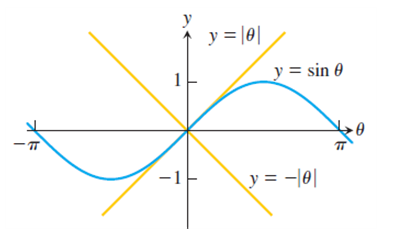
-|x|≤sinx≤|x|이므로, squeeze theorem을 이용하면, [식 1]이 성립[그림 5]함을 확인할 수 있다.
sinx/x의 극한
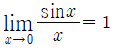
x 값을 극도록 줄일수록 0.999...로 계산된다.
sinπ/x의 극한
존재하지 않는다.
x^2(sin(1/x))의 극한
부등식의 관계 -1≤sin(1/x)≤1에 x^2을 곱하면,
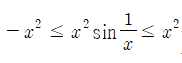
[식 3]을 얻을 수 있다.
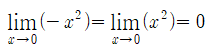
[식 4]에 근거해, [식 3]에 squeeze theorem을 적용하면, x^2(sin(1/x))은 0이라 할 수 있다.
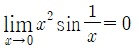
코사인 함수
cosx의 극한
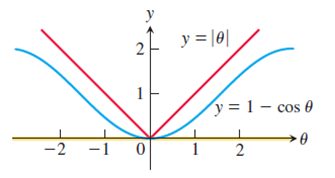
모든 x에 대해 0≤1-cosx≤|x|이므로, lim_{a→0}(1-cosx)=0이 성립하고, 극한법칙에 따라 lim_{a→0}cosx=1(식 5)을 유도할 수 있다.
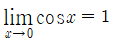
식 5
cosx-1/x의 극한
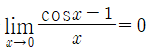
탄젠트 함수
tanx/x의 극한
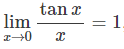
이외에도,
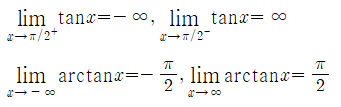
와 같은 탄젠트 함수 관련 극한 값들이 있다.
'미분적분학 > 미분' 카테고리의 다른 글
| 【미분적분학 1】 Chapter 11. 미분법: 다항함수 도함수 (0) | 2024.11.16 |
|---|---|
| 【미분적분학 1】 Chapter 10. 엡실론-델타 논법 (0) | 2024.11.15 |
| 【미분적분학 1】 Chapter 8. 적용: 극한의 성질 (1) | 2024.11.13 |
| 【미분적분학 1】 Chapter 7. 극한의 성질 (0) | 2024.11.12 |
| 【미분적분학 1】 Chapter 6. 함수의 연속성 (0) | 2024.11.11 |