직각좌표계는 이차원 상에서 원점 O를 기준으로 임의의 한 점 P를 P(x, y)로 표현한다. 한편, 평면 극좌표계(polar coordinate system)는 평면상의 한 점을 표현할 때, r과 θ를 사용해 점의 위치를 표현할 수 있다.
- 극좌표계는 고대 그리스의 천문학자 히파르코스(Hipparchus of Nicaea, c. B.C. 190~c. B.C. 120)가 남긴 각도에 따른 현(chord functions)의 기록으로부터 찾을 수 있다.

그림 3.1
- r: 직각 좌표의 원점으로부터 한 점의 특정 위치인 (x, y)까지의 거리
- θ: 원점에서 주어진 점까지 그은 선분과 고정된 좌표 x축 사이의 각도
- 고정 축은 일반적으로 +x축을 택하고, 각도는 반시계(counter-clockwise) 방향으로 잡는다. ⇒ 오른손을 기준으로 오른손가락을 감싸는 방향을 (+)방향으로 설정했다.
(1) +θ: +x축으로부터 반시계 방향의 각도
(2) -θ: +x축으로부터 시계 방향의 각도
삼각법과 삼각함수
삼각법은 평면 극좌표계로부터 직각좌표계를 수학적으로 얻기 위해 고안되었다.
- 삼각함수의 성질은 직각삼각형의 특성들로부터 유도된다.
- 삼각함수란, 각의 크기를 삼각비로 나타낸 함수로 예각 삼각함수는 직각 삼각형의 예각(acute angle)에 직각 삼각형의 두 변 길이의 비를 대응시킨다.

그림 3.2
삼각함수의 기본공식
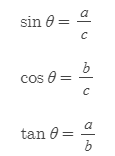
■
- a: 높이변(opposite), 각도 θ를 끼지 않은 변이다.
- b: 밑변(adjacent)
- c: 빗변(hypotenuse)
삼각함수의 기본공식에 따라 tan를 다음과 같이 쓸 수도 있다.

삼각함수의 각 값은 그에 상응하는 역수 값을 갖는다.
삼각함수의 역수(reciprocals)
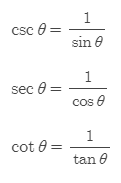
■
직각삼각형은, 또한, 피타고라스의 정리(Pythagorean theorem)를 따른다.
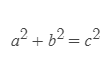
식을 변환하면 빗변의 길이 c를 다음과 같이 구할 수 있다.
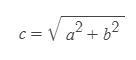
피타고라스의 정리를 활용해 피타고라스의 항등식(Pythagorean identity)을 유도할 수 있다.
피타고라스의 항등식

■
삼각함수의 성질
좌표계의 이해는 삼각함수의 성질을 이해하는 데서 출발한다.

그림 3.3
그림 3.3의 그래프를 통해 삼각함수의 기본성질을 다음과 같이 정리할 수 있다.
삼각함수의 기본성질
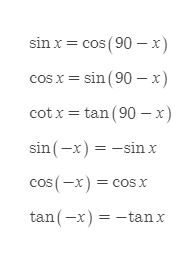
■
삼각함수의 관계식
피타고라스의 항등식처럼 삼각함수(사인함수, 코사인함수, 탄젠트 함수)는 서로 밀접한 관계를 관계식의 형태로 갖는다.
삼각함수의 관계식
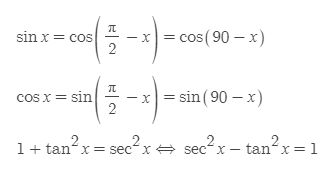
■
- π는 180도이다.
삼각함수의 덧셈정리
합곱변환식
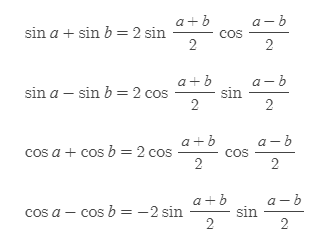
■
곱합변환식
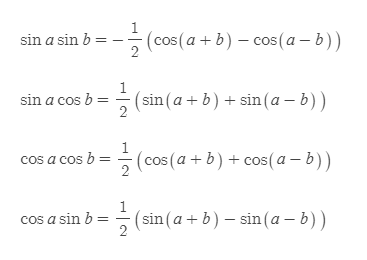
■
합곱변환식은 (삼각함수의) 합 식을 곱으로 변환하는 방법이고, 곱합변환식은 곱 식을 합으로 변환하는 방법이다.
- 삼각함수의 합곱, 곱합 변환식은 삼각함수의 가법을 통해 쉽게 유도할 수 있다.
삼각함수의 가법
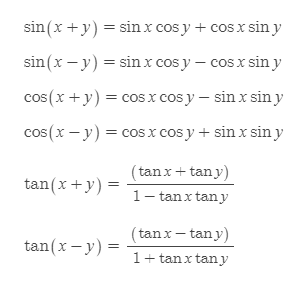
■
배각공식(double-angle formula)
마지막으로 삼각함수에서 중요한 배각공식을 알아보자.
Double-angle Formulas
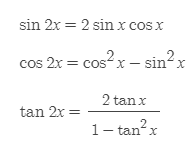
■
배각공식과 항등식을 활용해 다음 식을 유도할 수 있다.
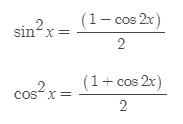
삼각형의 일반성질
직각삼각형이 아닌 일반적인 삼각형의 경우, 사인 법칙(law of sines)과 코사인 법칙(law of cosines)이 성립한다.
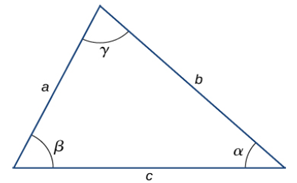
그림 3.4
Law of Sines
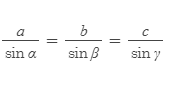
■
Law of Cosines
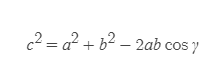
■
#물리학 #Physics #삼각법 #삼각함수 #삼각함수의성질 #피타고라스 #사인법칙 #코사인법칙 #배각공식 #합곱변환 #곱합변환
'고급물리학' 카테고리의 다른 글
| 뉴턴의 운동3법칙: 관성의 법칙 (0) | 2020.11.07 |
|---|---|
| 벡터량의 계산: 벡터의 사칙연산 (0) | 2019.12.28 |
| 물리인증제 기출 테마(2019) (0) | 2019.12.21 |
| 벡터량의 정의와 수 (0) | 2019.12.17 |
| 좌표계: 기초 (0) | 2019.12.14 |