우주의 법칙은 자연현상을 나타내는 물리량(physical quantities) 간의 수식들로 나타난다. 그리고 이 물리량은 '연산법'에 따라 2가지로 나뉜다.
- 물리량은 자연의 한 현상을 수로 대표한다.
1. 스칼라량(scalar quantities)
2. 벡터량(vector quantities)
두 가지 물리량은 자연 현상을 '몇 가지 수'로 정할 수 있느냐에 따라 서로 구분된다.
- 3차원 공간에서 일어나는 자연현상을 기술할 때, 3^0=1개의 수로 대표되는 물리량을 스칼라량이라고 한다.
- 같은 조건으로, 3^1=3개의 수로 대표되는 물리량을 벡터량이라고 한다.
n차원에서 스칼라의 조건과 벡터의 조건을 참고하도록 하자.
예를 들어 100도씨의 끓는 물은 다른 두 컵에 담겨져 있다고 해도, 모두 '1개의 (온도) 차원'으로 서로를 비교할 수 있다. 따라서 온도(temperature)는 스칼라량이다. 한편, 테이블에 놓인 네모난 주사위에 동쪽, 그리고 서쪽으로 각각 같은 '크기'의 힘을 주었다고 가정해보자. 이때 주사위는 힘을 준 '방향'으로 '가속'을 시작할텐데, 두 힘이 비록 같은 크기로 주어졌으나 그 결과가 같지 않으므로, 힘은 두 가지 수 이상을 고려해야하는 물리량, 즉 벡터량임을 알 수 있다.
크기와 방향, 그리고 수
2차원의 벡터

그림 2.1
물리량을 나타내는 경우, 벡터는 xy좌표 상 (기하학적으로) 화살표(그림 2.1)로 표현되며, (2차원 상에서 벡터는) '화살표의 방향'과 '화살표의 길이'로 양적으로 표현된다.
- 화살표의 방향과 벡터의 방향은 서로 일치한다.
- 화살표의 크기와 벡터의 크기는 서로 일치한다.
벡터 화살표가 시작되는 지점을 좌표계의 원점으로 잡으면, 벡터의 두 수는,
(1) 화살표의 길이와
(2) +x축에서 벡터 사이의 각 θ
라 할 수 있다. 즉, 벡터의 두 수를 알면 누구나 화살표를 그릴 수 있다.

컴포넌트 벡터: 각 축 방향성분으로 대표된 벡터

그림 2.2
벡터 A를 살펴보자.
- 벡터 A는 크기 A의 +x축과의 벡터 사이각을 갖는 벡터로 각 축의 방향성분으로 성분벡터로 분리할 수 있다.

- 화살표의 끝부분부터 x축으로 내린 수선이 x축과 만나는 점까지의 벡터 크기를 벡터 A sub x라고 한다.
- 화살표의 끝부분부터 y축으로 그은 수선이 y축과 만나는 점까지의 벡터 크기를 벡터 A sub y라고 한다.

2차원 벡터의 이 두 성분벡터(component vectors)을 알면 원점으로부터 뻗어나오는 벡터 A의 화살표를 그릴 수 있다.
2차원 상에서 벡터를 대표하는 두 수는 결국 다음과 같이 정리할 수 있다.
| 2차원 상의 벡터를 대표하는 두 수는 (1)벡터 크기, +x축과 벡터 화살표 사이각, 또는 (2) 벡터의 x, y축 방향 성분벡터들이다. |
3차원의 벡터

그림 2.3
3차원 공간에서 벡터는 3개의 수를 가지며, 세 가지 수는 다음과 같다.
- 벡터의 크기
- 극각
- 방위각
먼저, 극각이란 그림 2.3에서 각 θ로 벡터의 방향이 z-과 이루는 각이다. 한편, 방위각은 각 Φ로 xy평면에 투영한 선이 +x축과 이루는 각이다.
마찬가지로, 3차원 벡터의 컴포넌트 벡터 역시 3개로, 아래와 같은 관계식이 성립한다.
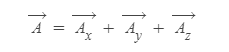
| 3차원 상의 벡터를 대표하는 세 수는 (1)벡터 크기, 극각, 방위각, 또는 (2) 벡터의 x, y, 그리고 z축 방향 성분벡터들이다. |
물리학에서의 스칼라량과 벡터량
물리학에서 등장하는 물리량은 스칼라량과 벡터량으로 나뉘며, 수적인 측면 이외에도 다음과 같은 특성을 공유한다.
스칼라량
1. 스칼라량은 좌표변환(coordinate transformation)에 의존하지 않는다. (Thornton, Classical Dynamics 5th edition)
2. 스칼라량끼리는 대수학적 산술 규칙(대수학적 계산)을 따른다.
3. 어떤 스칼라량은 음수부호를 갖는다. e.g. 음전하 -q
벡터량
1. 2차원 이상의 좌표계에서 벡터량은 특정한 '방향'을 가지며, 이에 따라 결과 값이 '각도'에 의존한다.
2. 벡터량끼리는 벡터연산을 따른다. ⇒ 수학적으로 벡터는 벡터공간(vector space; 벡터 연산이 가능한 공간)의 원소로서 정의된다.
- 벡터의 수학적 연산은 (1)좌표계의 설정 이후 (2)벡터의 수끼리 연산하는 방식이다.
made by sortie
ⓒAll Rights Reserved
'고급물리학' 카테고리의 다른 글
| 뉴턴의 운동3법칙: 관성의 법칙 (0) | 2020.11.07 |
|---|---|
| 벡터량의 계산: 벡터의 사칙연산 (0) | 2019.12.28 |
| 물리인증제 기출 테마(2019) (0) | 2019.12.21 |
| 벡터량의 계산: 삼각법(Trigonometry) (0) | 2019.12.19 |
| 좌표계: 기초 (0) | 2019.12.14 |

