
s orbital은 l=0, m=0인 ψ_nlm 함수이다. 모든 s 궤도함수에서 각도 부분인 Y는 상수 값이다.

- s 오비탈은 θ와 φ 값에 의존하지 않기 때문에, 핵을 중심으로 구면 대칭성을 갖는다.
- s 오비탈의 진폭은 핵으로부터의 거리 r만의 함수이고, 방향과는 무관하다.

그림 1. 수소원자가 1s, 2s, 3s 상태에 있을 때 전자의 확률밀도, 이들 그래프를 제곱하면 파동함수의 제곱을 가시적으로 구할 수 있다.
파동함수 그래프를 통해 우리는 파동함수의 값이 0이 되는 지점을 알 수 있는데, 이곳이 바로 node이다. s 오비탈의 경우, 파동함수의 그래프에서 방사 노드(radial node)를 확인할 수 있다.

그림 2. 확률밀도와 파동함수의 제곱 그래프
- 파동함수 그래프에서 node는 양의 위상(phase)을 갖는 부분과 음의 위상을 갖는 부분의 경계이다.
방사확률밀도(radial probability density)

그림 3. 방사파동함수의 제곱에 r^2을 곱한 방사확률밀도
방사확률밀도(radial probability density, radial distribution function)란 핵으로부터 떨어진 거리 r만큼, 모든 각도 θ, φ 값을 포함한 영역에서 전자를 발견할 확률밀도를 의미한다.
- radial distribution function은 핵으로부터 거리 r에 위치한, 두께가 dr인 얇은 구면 껍질 안에서 전자를 발견할 확률을 의미한다.

그림 4. 전자가 r에서 r+dr 사이의 구각에서 발견될 확률
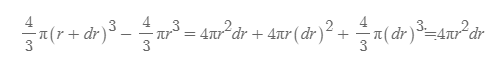
- dr은 r에 비해 충분히 미소한 구간이고 이를 제곱하거나 세제곱하면 그 크기가 더욱 작아지므로 그 값을 무시할 수 있게 된다.
- s orbital의 구각에서 전자가 발견될 확률은 일정 구각의 부피에 파동함수의 제곱의 곱으로 정의한다.


방사확률밀도는 2가지 경향성을 갖는다.
1. 핵에서 멀어질수록 전자의 발견확률은 감소한다.
2. 구면껍질 내의 확률밀도를 더할 때 이 껍질의 부피는 거리가 증가할수록 증가한다.
두 가지 경향성은 서로 경쟁하며 이 두 경향성의 효과에 의해 방사확률함수가 어떤 거리에서 최대값이 되는 지 결정된다.
s 궤도함수의 크기
원자의 크기는 그 안에서 전자를 발견할 확률이 90% 이상인 면의 영역으로 정의한다. 수소원자의 1s, 2s, 3s 궤도함수의 90% 구 반지름(영역)은 다음과 같다.
- 1s: 1.41 옴스트롱
- 2s: 4.83 옴스트롱
- 3s: 10.29 옴스트롱
ns의 n이 증가함에 따라 궤도의 반지름이 증가하는 것을 확인할 수 있다. 또한 n이 커질수록 전자발견확률이 최대인 지점이 핵으로부터 멀어진다.
- 2s, 3s 궤도함수에서 핵에서 전자를 발견할 수 있는 확률이 0이 아니다! 왜냐하면 s 궤도함수에 있는 전자들은 각운동량이 0이므로 방사상 방향을 따라 핵에 접근할 수 있기 때문이다.
- s 궤도함수의 전자는 핵에 '침투'할 수 있고 이는 다전자 원자와 분자의 구조에 큰 영향을 끼친다.
ns 궤도함수는 n-1의 radial node를 갖는다.
'대학화학' 카테고리의 다른 글
| [G. Chem] 16. 이온화에너지(Ionization Energy) (0) | 2020.04.05 |
|---|---|
| [일반화학] 15. p 궤도함수(p 오비탈) [심화] (0) | 2020.03.04 |
| [일반화학] 13. 수소원자의 분석 [심화] (0) | 2020.03.04 |
| [일반화학] 12. 원자 반지름과 이온 반지름 (0) | 2020.03.04 |
| [일반화학] 11. 전자배치도 (0) | 2020.03.01 |