
운동에너지(Kinetic Energy)
외력(external force)에 의한 물체에 한 work는 물체의 변위를 만들고, 속력의 변화를 수반한다.
- 일은 system에 대해 에너지를 역학적으로 전달하는 형태로 나타난다.
Newton's second law와 work 식 조합
'뉴턴의 운동 제 2법칙'과 '힘의 x성분이 변화하고 직선 변위일 때 일' 식을 조합하면 운동에너지(kinetic energy)의 개념을 유도할 수 있다.
▼ Reference: Newton's Second Law with the Inertial Mass
https://blog.naver.com/sortie0228/221922644363

[Mechanics] 질량과 무게 | Mass and Weight
힘에 관한 흔한 예로 물체의 무게(weight)를 들 수 있는데, 이는 지구가 물체에 작용하는 중력이다. 그런...
blog.naver.com
▼ Reference: 힘의 x성분이 변화하고 직선 변위일 때 일
https://blog.naver.com/sortie0228/221924130429

[Mechanics] 일과 에너지 | Work and Energy
일과 에너지energy: 물리계가 일(work)을 얼마나 할 수 있는 지를 정량적으로 표현한 값- 에너지는 직접 ...
blog.naver.com
[1] 1차원으로 물체의 운동을 한정했을 때, 뉴턴의 운동 제 2법칙과 일정하지 않은 힘이 주어질 때 일의 적분 표현은 다음과 같다.
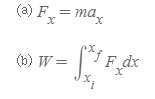
[2] (a)를 (b)의 F_x식에 대입하여 적분 식을 풀 수 있다.

- 가속도 a는 운동학에서 흔히 dv/dt로 표현된다.
[3] 적분 식의 풀이를 위해 연쇄법칙(chain rule)을 사용한다.

[4] 결국 W는 다음과 같이 요약할 수 있다.
외력에 의한 일의 공식

- 외력에 의한 양(+)의 일은 물체의 속력증가로 나타난다.
■
Total Work
하나의 물체에 여러 가지 힘이 작용할 때 이 힘들이 물체에 한 일을 전체 일(총 일)이라 한다.
- 전체 일에서 힘은 알짜힘을 의미한다.
Total Work

■

운동에너지(Kinetic Energy, KE)의 정의

- 운동에너지는 입자의 운동으로 나타나는 수치화된 에너지를 의미한다.
- 운동에너지는 일과 마찬가지로 스칼라량이다. ⇒ 운동에너지는 결코 음의 값이 될 수 없다. e.g. 북쪽으로 10m/s로 움직이는 자동차나 남쪽으로 10m/s로 움직이는 자동차는 모두 1/2(m)(100)의 운동에너지를 가진다.
- 단위: J(joule)
■
Properties of Kinetic Energy
1. 움직이는 물체의 질량과 속력이 같다면, 움직이는 방향과 무관하게 운동에너지는 서로 같다.
2. 물체의 질량이 2배(2m)라면 운동에너지는 질량 m의 물체의 운동에너지에 비해 2배 더 크다.
3. 물체의 속력이 2배(2v) 증가하면 운동에너지는 속력 v의 물체의 운동에너지에 비해 '제곱 배'인 4배 만큼 더 크다.

그림 1. PE는 KE로 변환될 수 있다. (PE can be transformed into KE.)
일-운동에너지 정리
어떤 계에 일이 가해지고 이 system의 유일한 변화가 속력뿐이라면, 알짜힘이 계에 한 일은 곧 계의 운동에너지 변화이다.
Work-Kinetic Energy Theorem(W-KE theorem)

■
W-KE theorem에서 ΔK는 처음과 나중 위치에서의 속력에만 의존하는 물리량이다.
- 두 점 사이의 이동경로에서 발생한 중간 속력은 ΔK값에 영향을 주지 않는다. 즉, 역학적 일과 운동에너지는 경로로부터 독립한 물리량이다.
- W-KE theorem의 W는 총 일(W_total, W_tot)을 의미한다.

또한, W-KE theorem에 의하면 물체의 최종운동에너지는 다음과 같이 계산할 수 있다.
Final Kinetic Energy

■
EXAMPLE 1.
양성자의 질량은 전자의 질량에 비해 약 1836배 더 크다. 양성자의 속력이 v일 때 전자가 양성자와 같은 크기의 운동에너지를 가지려면 (전자의)속력이 얼마가 되어야 하는 지 구하시오.
□
EXAMPLE 2.
무게가 10N인 물체를 지표면으로부터 수직으로 던져 올렸다. 돌이 땅으로부터 20.0m 높이에 있을 때, 돌은 위쪽으로 30.0m/s로 움직였다고 하자. 이 때 돌의 초기속력과 최대 높이를 work-energy theorem을 이용해 구하시오.
□
EXAMPLE 3.
정지 상태의 질량이 5.00kg인 물체가 높이가 25.0m인 지점에서부터 떨어졌다.
(단, 공기 저항은 없다.)
(a) 물체가 떨어질 때 중력이 한 일은 얼마인가?
(b) 물체가 지표면에 닿기 전 물체의 운동에너지와 속력을 구하시오.
(c) 만약 공기저항이 있다면, (a)와 (b)의 값은 어떻게 달라지는가?
□
EXAMPLE 4.
소총 탄환이 +x축을 향해 350m/s의 속력으로 날아와 나무 토막에 0.10m의 깊이로 박혔다. 탄환의 질량은 1.80g이었고, 나무가 탄환에 작용한 힘은 일정했다.
(a) 탄환이 정지하는 데 걸린 시간은 얼마인가?
(b) 나무는 탄환에 몇 뉴턴의 힘을 주었는가?
□
EXAMPLE 5.

그림 2
질량이 3kg인 물체가 x축의 직선 경로로 움직이고 있다. [그림 2]은 시간에 따른 물체의 x축 성분 속도를 나타낸다.
(a) 물체에 작용하는 최대 알짜힘을 구하시오.
(b) 8.5초에서 주어진 알짜힘은 얼마인가?
□
EXAMPLE 6.
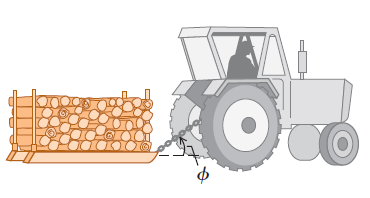
그림 3
장작을 실은 트랙터가 수평방향으로 20m만큼 움직였다. 트랙터가 끄는 썰매와 장작 짐의 전체 무게는 15,000N이다.
- 트랙터는 수평면에 대해 36.9도의 각도로 5,000N의 힘을 일정하게 작용하고 있다.
- 썰매의 운동방향의 반대쪽으로 마찰력이 3,500N이 작용하고 있다.
썰매에 작용하는 각각의 힘이 한 일과 모든 힘이 한 전체 일을 구하시오.
□
EXAMPLE 7.

그림 4
질량이 200kg인 강철 해머가 수직으로 세워진 I빔의 위쪽으로 3.00m의 높이에 위치해 있다. 해머가 떨어지면 I빔은 땅 속으로 7.4cm의 깊이로 박힌다.
- 해머가 따라 내려오는 수직 레일은 60N의 일정한 마찰력을 작용한다.
(a) 해머가 I빔을 때릴 때 속력은 얼마인가?
(b) 해머가 I빔을 때릴 때 작용하는 평균 힘은 얼마인가?
단, 공기저항은 무시한다.
□
EXAMPLE 8.

그림 5
어떤 아이가 스케이트보드를 타고 3.00m 반지름의 4분원 경사로를 따라 내려오고 있다. 아이의 질량이 25.0kg일 때,
(a) 바닥에서의 속력
(b) 아이가 바닥에 안착했을 때, 수직항력이 이 아이에게 가하는 힘을 구하시오.
□
EXAMPLE 9.

그림 6
어떤 물체가 x=0에서 정지해 있다. Work-Energy Theorem을 이용해 다음 위치에서의 물체의 속력을 구하시오.
(a) x=8.0m
(b) x=12.0m
□
#물리학 #대학물리학 #일 #운동에너지 #운동에너지변화량 #일운동에너지정리 #최종운동에너지 #연쇄법칙
'고급물리학 > 고전역학' 카테고리의 다른 글
| [Mechanics] 탈출 속도 | Escape Velocity (0) | 2020.05.01 |
|---|---|
| [Mechanics] 역학적 에너지 보존법칙 | Conservation of Mechanical Energy (0) | 2020.04.30 |
| [Mechanics] 중력 퍼텐셜에너지 공식 유도 | Derivations of Gravitational Potential Energy (1) | 2020.04.30 |
| [물리학-고전역학] 02. 기본물리량 - 길이, 질량, 시간 | Length, Mass, and Time (0) | 2020.04.30 |
| [물리학-고전역학] 01. 물리학에 관하여 | What is Physics (0) | 2020.04.23 |