음함수 미분법
지금까지 미분법을 위한 함수는 y=f(x)의 꼴을 가졌다. 즉, 우변에 x항을 모두 모은 형태로 이전 장까지는 양함수(explicit function)에 대한 미분법만을 다루었다.
- where the variable y is on the left side, and the right side depends only on the independent variable x, then the function is said to be an explicit function(or be given explicitly).
그러나,

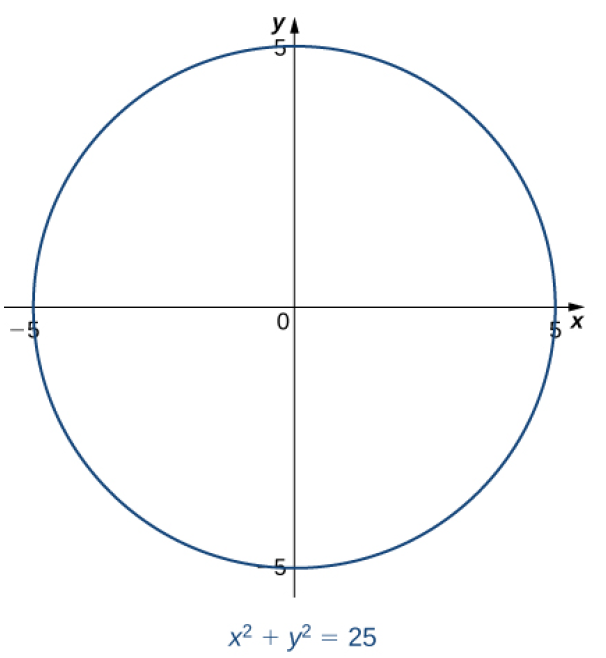
와 같은 함수는 y=f(x) 꼴로 y를 표현할 수 없다. 즉, 식 10.1은 음함수적(implicitly)으로 표현될 수 있다고 정의한다.
음함수를 정의하기 위해 식 10.2를 가정하자.

식 10.2는 음함수의 정의에 의해 다음과 같이 변한다.
음함수

■
therefore,

식 10.3은 식 10.2의 음함수의 정의에 따라 새롭게 고친 식으로, 이제 음함수 미분법(implicit differentiation)을 이용해 음함수인 식 10.3의 y'을 구할 수 있게 된다.
- y는 x에 대해 미분할 수 있는 함수라는 전제(음함수 미분법의 전제)가 붙는다. ⇒ 음함수로 재구성된 식은 음함수의 정의에 따라 y를 x에 대해 정리할 수 있다.
음함수가 F(x, y)라면, y는 x에 대해 미분가능이라 간주하고, 양변을 x에 대해 미분한다.
음함수 미분법의 전략
음함수 미분법의 전제를 만족하는 음함수의 정의 f(x, y)=0에 대해 y'은 다음과 같이 구한다.

음함수 미분법의 전략은 밑이 a인 로그함수의 도함수를 구하는 데 쓰인다.
PROOF. 밑이 a인 로그함수의 도함수

□
음함수 미분법은 아이작 뉴턴에 의해 고안되었다.
로그 미분법
여러 가지 연산이 함께 주어지는 복잡한 함수의 도함수는 로그를 취하여 간단히 구할 수 있다.
로그 미분법
[1] y=f(x)의 양변에 자연로그를 취하여 복잡한 합성함수를 먼저 간단히 한다.
[2] x에 대해 음함수 미분법을 수행한다.
[3] y'에 대해 최종적으로 푼다.
EXAMPLE 10.1 로그 미분법
다음 합성함수의 y'을 구하시오.

SOLUTION.

답은 y'=y[(3/2x)+(x/x^2+1)-(12/3x+2)]이다.
□
'Calculus > Concepts of Calculus' 카테고리의 다른 글
| [적분] 12장. 적분: 정적분 (0) | 2019.08.27 |
|---|---|
| [적분] 11장. 적분: 입문 (0) | 2019.08.27 |
| [미분] 9장. 도함수: 지수함수와 로그함수의 도함수 (0) | 2019.08.25 |
| [미분] 8장. 도함수: 삼각함수의 도함수 (0) | 2019.08.25 |
| [미분] 7장. 도함수: 곱법칙과 몫법칙, 그리고 연쇄법칙 (0) | 2019.08.25 |