Herald-Lab
[미분] 7장. 도함수: 곱법칙과 몫법칙, 그리고 연쇄법칙 본문
곱법칙
함수(구함수) f와 g가 모두 미분가능일 때, 함수들을 곱하거나 나누어 얻어지는 새로운 함수의 도함수 역시 구할 수 있다.
먼저, 곱법칙(product rule)은 두 구함수를 곱하여 얻은 새로운 함수의 도함수를 구하는 방법이다.
곱법칙
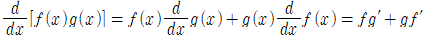
■
- 두 함수의 곱의 도함수는 앞의 함수에 뒤의 함수의 도함수를 곱한 값에, 뒤의 함수에 앞의 함수의 도함수를 곱한 값 둘을 더한 것과 같다.
몫법칙
한편, 몫법칙(quotient rule)은 두 함수를 나누어 얻은 새로운 함수의 도함수를 구하는 방법이다.
몫법칙

■
연쇄법칙
연쇄법칙은 합성함수(composition of two functions)를 미분하는 방법이다.
만약,
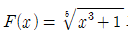
와 같은 함수를 미분할 경우, 지금까지 배운 미분공식으로는 이를 풀 수 없을 것이다. 이때, y=f(u)=5√u, u=g(x)=x^3+1로 두면, y=F(x)=f(u)=f(g(x))로 고쳐 쓸 수 있다.
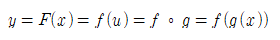
연쇄법칙(chain rule)

■
라이프니츠 기호로 chain rule을 쓰면 다음과 같다:
dy/dx = (dy/du)(du/dx)
- y는 u의 함수이고, u는 x의 함수이다.
- 연쇄법칙은 다음과 같은 풀이전략을 갖는다.
[1] 합성함수가 h(x)=f(g(x)) 꼴 일 경우, f(x)와 g(x)를 먼저 규명(identifying)한다.
[2] f'(x)를 구한다.
[3] f'(g(x))를 구한다.
[4] g'(x)를 구한다.
[5] h'(x)은 f'(g(x))g'(x)이다.
Write h'(x)=f'(g(x))g'(x) down as the solution.
※ 미분 성질의 발견
1. 곱법칙: 일반적으로 곱법칙은 라이프니츠를 발견자로 인정하고 있다. 그러나 라이프니츠의 저작물을 번역한 J. M. Child과 같은 학자들은 발견자로 뉴턴의 스승 아이작 배로(Isaac Barrow, 1630~1677)를 지목하기도 한다.

라이프니츠는 곱법칙을 다음과 같이 작성했다.
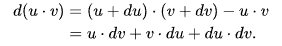
여기서 dudv는 du와 dv에 비해 그 크기가 무시될 수 있는(negligible) 값이었기에 라이프니츠는 최종적으로 곱법칙을 다음과 같이 정의했다.
d(uv)=vdu+udv
라이프니츠는 d/dx를 d로 축약하여 작성하였으므로:

풀어 쓸 수 있다.
2. 연쇄법칙: 연쇄법칙은 라이프니츠에 의해 처음으로 언급(1676 memoir)되었다.
'Calculus > Concepts of Calculus' 카테고리의 다른 글
| [미분] 9장. 도함수: 지수함수와 로그함수의 도함수 (0) | 2019.08.25 |
|---|---|
| [미분] 8장. 도함수: 삼각함수의 도함수 (0) | 2019.08.25 |
| [미분] 6장. 도함수: 다항함수의 도함수 (0) | 2019.08.25 |
| [미분] 5장. 도함수: 입문 (0) | 2019.08.24 |
| [미분] 4장. 점에서의 변화율 (0) | 2019.08.24 |





