Herald-Lab
[미분] 5장. 도함수: 입문 본문
미분계수에서 a(점 P의 x값)는 고정된 값이었다. 그러나 도함수(derivative)를 정의하기 위해 a를 '이동'시킨다. 미분계수 식에서 a를 변수(variable) x로 바꾼다.
도함수(derivative)
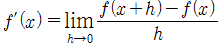
■
x지점에서 f'의 값은 기하학적으로 점 (x, f'(x))에서 f의 그래프에 접하는 접선의 기울기이다.
- f'(x)는 f의 derivative(of f)라는 새로운 함수로 정의된다.
- f'(x)의 정의역은 f의 정의역보다 크지 않다.
EXAMPLE 5.1 도함수
함수가 f(x)로 주어졌을 때, f'(x)를 구하시오.

SOLUTION.
f(x)를 f'(x) 식에 대입하기 위해 f(x+h)를 구해야 한다. f(x+h)를 구한 이후에 도함수 식에 각 항을 대입하면 f'(x)를 쉽게 구할 수 있다.
(1)

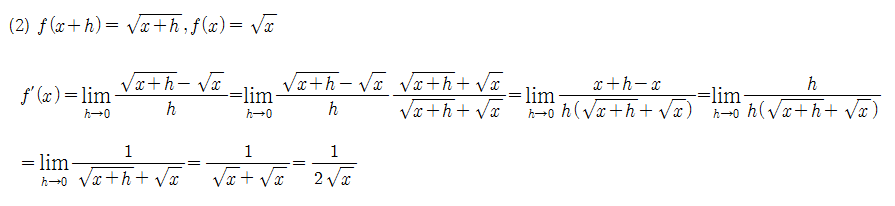

■
도함수는 모든 미분의 가장 근본적인 원리이다. 그러나 위의 계산과정은 너무나 많은 시간을 필요로 하고, 또한 복잡하다. 따라서 이런 수고를 덜기 위해 '미분법'을 공부해야 하고, 수많은 예제 풀이를 통해 패턴을 학습(및 암기)함으로써 미분을 기계적으로 할 수 있게 된다.
자주 사용되는 함수-미분 공식
미분은 다양한 함수에 대한 도함수를 구하는 과정으로, 다른 함수의 도함수 또한 같은 방식으로 유도되었다. 많이 사용되는 함수의 미분 공식은 예제를 풀이하면서 암기하도록 하자.

미적분학의 시작
역사적으로, 미분과 적분은 (수많은 수학자들에 의해) 독립적으로 발달했다. 그러나 현재 우리가 배우는 미적분학의 학문적 기반은 영국의 자연철학자 뉴턴(Isaac Newton, 1643~1727)과 독일의 법학자 라이프니츠(Gottfried Leibniz, 1646~1716)의 공헌이 가장 크다.
- 뉴턴은 1665년에서 1666년 사이에 미분법을 물리학 연구를 위한 개인적인 도구로 사용했다. 그러나 논문으로 작성하지 않았다.
- 뉴턴은 먼저 라이프니츠에게 미분의 기본적인 개념을 설명했다. ⇒ 자연철학자로서 뉴턴은 속도(velocity)와 가속도(acceleration)를 자신의 미분 표기법(Newton's dot notation)으로 설명했다.
- 라이프니츠는 뉴턴의 물리학적 설명 대신, 접선의 개념으로 미분을 엄밀히 설명했다.
- 또한, 라이프니츠는 자신의 저서 『미적분학의 해석』(1684)에서 도함수의 기호와 표기 패턴을 소개했다. 또한 적분의 integral 기호 및 표기법도 고안했다.
Legacy
Newton introduced the notation dot notation.
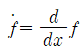
for the derivative of a function f.
Meanwhile, Leibniz introduced the symbol,

for the integral and wrote the derivative of a function y of the variable x as:
dy/dx(Leibniz notation), which is still in use.


'Calculus > Concepts of Calculus' 카테고리의 다른 글
| [미분] 7장. 도함수: 곱법칙과 몫법칙, 그리고 연쇄법칙 (0) | 2019.08.25 |
|---|---|
| [미분] 6장. 도함수: 다항함수의 도함수 (0) | 2019.08.25 |
| [미분] 4장. 점에서의 변화율 (0) | 2019.08.24 |
| [미분] 2장. 함수의 극한 (0) | 2019.08.24 |
| [미분] 1장. 미분적분학 들어가기: 접선과 넓이 (0) | 2019.08.24 |





