Herald-Lab
[미분] 2장. 함수의 극한 본문
미분을 공부함에 있어, 극한(limit)의 개념은 매우 중요하다.
예를 들어, 다음과 같은 극한 식이 있다고 하자.

주어진 식 2.1은 다음과 같이 정의한다.
극한(limit)
a와 같진 않으나, a에 충분히 가까운 x 값을 잡으면 L에 얼마든지 가까운 f(x) 값을 얻을 수 있는데, 'x가 a에 접근할 때, f(x)의 극한을 L'이라 한다.
■
The definition of the limit
If all values of the functions f(x) approach the real number L as the value of x (not equal to a) approaches the number a, then we can say that the limit of f(x) as x approaches a is L.
x가 a에 접근할 때, f(x)의 값은 L에 가까워지는 데, 단 x는 a가 되지 않음에 유의한다.
※ 엄밀한 극한의 정의는 【엡실론-델타 논법】에서 다루어지며, 자세한 내용은 링크를 참조하도록 하자.
https://herald-lab.tistory.com/18
엡실론-델타 논법
17세기 미적분학이 '발명'된 이후, 여러 수학자들에 의해 실용적인 발전을 거쳤다. 그러다 19세기에 이르러 미적분학은 '엄밀한 정의'의 재정립이 필요했는데, 이러한 움직임의 선두 주자로 프랑스의 수학자 코시..
herald-lab.tistory.com
좌극한과 우극한
좌극한(limit from the left, left-hand limit): a보다 작으면서 a에 충분히 가깝도록 x를 설정하면, f(x)의 값이 L에 가까워지는 데, 이 때 x→a인 경우, f(x)의 좌극한은 L이라 한다.

우극한(limit from the right, right-hand limit): a보다 크면서 a에 충분히 가깝도록 x를 설정하면, f(x)의 값이 L이 가까워지는 데, 이 때 x→a인 경우, f(x)의 우극한은 L이라 한다.


좌극한과 우극한은 c를 향한다는 공통점 때문에 일방향 극한(one-sided limit)으로 묶어 부르며, 좌극한은 그래프의 '왼쪽'에서 출발하여 오른 방향으로 움직이며, 우극한은 '오른쪽'에서 출발하여 왼 방향으로 움직인다.
일방향성 극한을 정의했고, 이 둘을 이용하면 극한의 필요충분조건을 정의할 수 있다.
극한의 필요충분조건(necessary and sufficient condition of the limit)

■
EXAMPLE 2.1 Heaviside 함수
영국의 전기공학자 헤비사이드(Oliver Heaviside, 1850~1925)가 고안한 헤비사이드 함수는 전기 스위치를 켤 때, 전류의 흐름을 나타낸다. t=0에서 스위치를 켤 때 전류는 거의 즉각적으로 도선을 타고 흐르는데, 이 때 그래프는 아래와 같다.

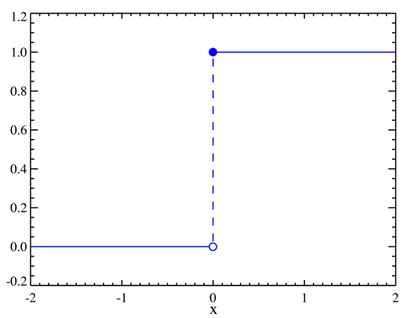
헤비사이드 함수 도식을 통해 좌극한과 우극한을 각각 구하시오.
SOLUTION.

헤비사이드 함수 도식에서 극한의 필요충분조건은 일방향의 극한 값들이 서로 일치하지 않으므로, 존재하지 않는다.
■
좌극한과 우극한이 같은 점에 있을 때, 함수의 극한 값이 존재한다고 한다.
- 임의의 x→a에서 좌극한의 값과 우극한의 값이 서로 같다면, 함수의 양방향 극한(2 sided-limit)이 존재한다.
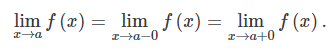
'Calculus > Concepts of Calculus' 카테고리의 다른 글
| [미분] 7장. 도함수: 곱법칙과 몫법칙, 그리고 연쇄법칙 (0) | 2019.08.25 |
|---|---|
| [미분] 6장. 도함수: 다항함수의 도함수 (0) | 2019.08.25 |
| [미분] 5장. 도함수: 입문 (0) | 2019.08.24 |
| [미분] 4장. 점에서의 변화율 (0) | 2019.08.24 |
| [미분] 1장. 미분적분학 들어가기: 접선과 넓이 (0) | 2019.08.24 |





