
확률 Probability
계와 변화과정에 대한 정보가 한정된 경우, 측정의 결과를 해석하거나 예측하는 데 있어 ‘확률’을 정하는 것은 매우 중요하다.
- 원자의 구조를 논의할 때 원자핵에 대한 전자의 상대적 위치 ⇒ 양자역학에 의하면 전자의 정확한 위치 혹은 궤적은 절대 알 수 없다. 대신 이에 대한 최적의 데이터로 원자핵 주위의 공간에서 전자를 발견할 확률을 물리량으로 사용할 수 있다.
- 특정한 부피와 압력, 그리고 온도 속에서 이상기체의 전반적인 거동을 설명할 때, 이상기체의 용기 속 움직이는 속력은 ‘분포도’로 표현할 수 있다. ⇒ 입자가 가능한 특정 속력을 움직임에 대한 확률로 추정
무작위 변수
무작위 변수(random variable): 실험에서 측정하고자 하는 물리량으로 실험을 여러 번 반복함에 따라 수치가 오르내린다. X로 표기한다.
결과(outcomes): 무작위 변수를 정의하고 여러 번 반복 수행함에 따라 X가 가질 수 있는 가능 값
동전 던지기
- X: 보이는 동전의 면
- 동전 던지기의 가능한 결과는 다음과 같다.
앞면, 뒷면
cf. 주사위를 던지는 경우, 결과는 총 1~6까지의 숫자이다.
확률함수
확률모형을 분석하는 데 가장 보편적인 방법은 결과를 임의의 그래프의 x-상에 나열하는 것이다. ⇒ 무작위 변수를 직교 좌표계의 수평축을 따라 표기한다.
- X의 특성은 연속적이거나 혹은 불연속적이다.
- 확률변수 X에 대해 확률을 나타내는 P(X)를 수직 축을 따라 도시한다.
확률함수(probability function): P(X), 확률변수 X를 반복하여 측정하고 그 결과를 히스토그램에 기록함으로써 생성되는 정보유형
30명의 학생이 20점이 만점인 물리 수행평가를 진행
학생은 0점에서 20점까지 자연수 단위로 채점되며, 이때 숫자는 무작위 변수에 대해 가능한 구체적 결과이다.
- 채점한 시험지는 총 30장으로 30번의 ‘실험반복’을 한 것과 동일하다.
- 위의 조건에서, 어떤 특정 점수를 받을 확률은 다음과 같이 정의한다.

잦음 값(probable value): 실험 데이터 중 가장 자주 나타나는 값, X_mp(most probable)
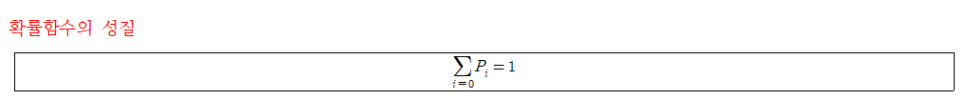
- 의미: 확률의 식을 통해 계산된 숫자는 절대 1을 넘지 않는다.
- 확률 함수의 매우 중요한 성질로 가능한 모든 결과에 대한 확률의 총합은 무조건 1이다.
확률함수의 성질을 만족하는 확률함수는 정규화(normalization)되었다고 표현한다. ⇒ 정규화는 주어진 상황에서 일어날 모든 가능한 결과에 대해 고려하고 있음을 의미하며 임의의 값을 받을 확률은 결국 1로 계산된다.
평균
평균(mean, average value): X bar, 각각의 가능한 결과에 이들의 확률을 곱한 값을 모든 가능한 결과에 대해 합하여 계산한다.
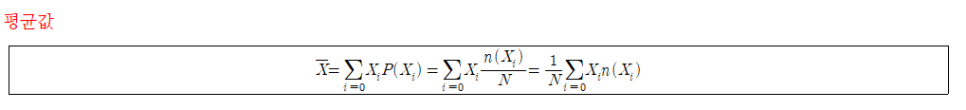
확률밀도 Probability Density


- 의미: 확률밀도함수와 특정구간에서의 미소간격의 곱의 적분 값은 1이다. 즉, 모든 가능한 경우의 확률을 더했을 때 그 값이 1을 넘지 않는다.
따라서, 특정 구간에서의 확률을 위의 식으로 구할 수 있다.
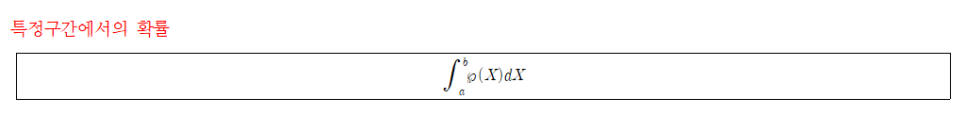
확률 밀도의 평균 역시 평균값 식을 응용하여 다음과 같이 계산한다.
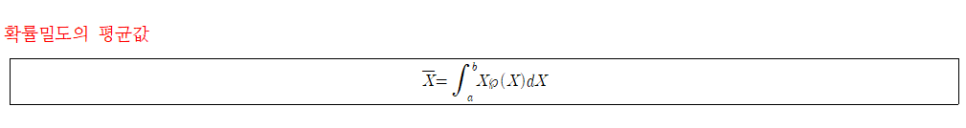
보른의 해석
폴란드-독일 태생의 영국의 물리학자 보른(Max Born, 1882~1970)은 입자의 파동함수를 위치에 따라 해석할 수 있다고 생각했다.
1. 한 영역에서의 전자기파 복사의 진폭의 제곱은 복사파의 세기와 같다.
- 전자기 복사가 있는 경우, 주어진 시간과 공간에 대해 단위 부피당 광자 하나를 찾을 수 있는 확률은 그 시간에서 단위 부피 당 광자의 수에 비례한다.
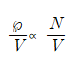
- Ρ: 단일한 광자를 찾을 수 있는 확률
2. 단위 부피당 광자의 수는 복사의 세기에 비례한다.
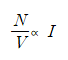
3. 전자기 복사의 세기는 전자기파에 대한 전기장의 진폭의 제곱에 비례한다.
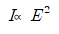
그러므로 비례식을 연결하면 다음과 같은 관계가 도출된다.
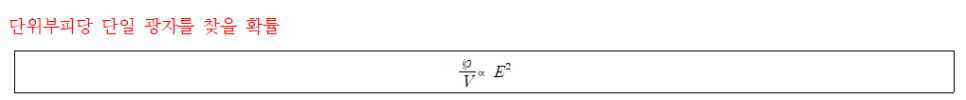
- 의미: 전자기 복사에서 복사와 관련한 입자를 찾을 단위 부피당 확률은 입자를 표현한 파동진폭의 제곱에 ‘비례’한다.
전자기파와 물질의 파동-입자 이중성을 인식하면서, 물질 입자에 대해서도 마찬가지로 비례성이 성립함을 추론할 수 있다. 즉, 입자를 찾을 단위 부피당 확률은 입자를 표현한 파동 진폭의 제곱에 비례한다.
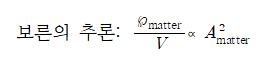
▶A_matter: 입자를 표현한 물질파 진폭 ⇒ 입자의 파동진폭을 확률 진폭(probability amplitude) 혹은 파동함수(wave function)라 하며 앞선 기호 ψ와 물리적인 의미가 같다.
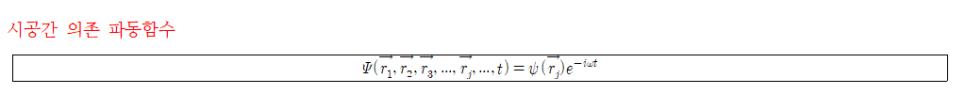
▶의미: 일반적으로 계에 대한 완전한 파동함수는 모든 입자의 위치와 시간에 동시에 의존한다. 여기서 벡터 r_j는 계에서 j번째 입자의 위치벡터이다.
많은 계에서 파동함수 ψ는 수학적으로 시공간에서 분리할 수 있고, 계의 입자들의 위치에 대한 복소공간함수 ψ와 복소시간함수 e^-iωt의 곱으로 쓸 수 있다!

복소시간함수에 복소수의 형태가 단적으로 드러난다.


퍼텐셜에너지를 가진 어떤 계가 시간과는 무관하고 단지 계 내부의 입자 위치에만 의존하는 경우, 계의 중요한 정보는 파동 함수의 공간항에 담겨있다!
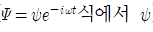
▶계의 시간은 복소수가 들어있는 e^-iωt이었으므로, 사실상 ψ만 분석하면 된다.
▶파동함수의 제곱절대치는 항상 실수이고 양수 값이다.
켤레 복소수
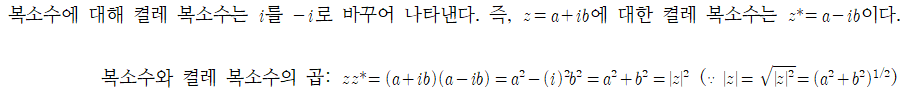
제곱 절대치

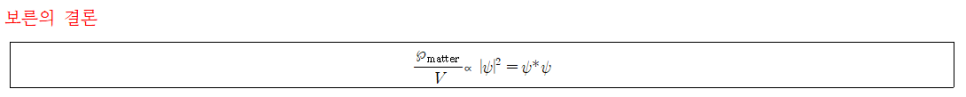
이상적인 자유입자가 정확하게 p_x의 운동량을 가진다면, 그 파동함수는 파장 λ=h/p_x의 사인형 함수이고 입자는 x-을 따르는 어느 점에 있을 확률과 같다.
확률밀도(probability density): 파동함수가 단일입자를 표현한다면, 파동함수의 제곱 절대치는 단위 부피당 주어진 점에서 입자가 발견될 확률에 비례하는 물리량이다.
PROOF. 파동함수의 규격화
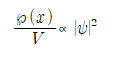
위의 식에 대해 단위 부피를 미소부피요소로 줄이면 식은 다음과 같이 수정된다.
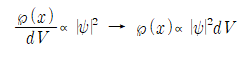
x-만을 움직이는 일차원계는 미소부피요소대신 dx로 고칠 수 있다.
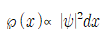
입자가 축을 따라 어딘가에는 반드시 존재해야 되는 데 x=0을 기점으로 입자는 -∞부터 +∞까지 이동할 수 있다.
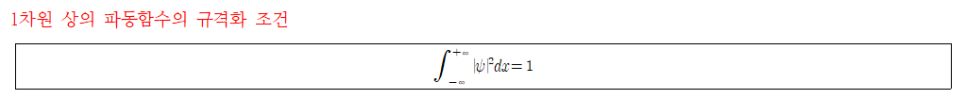
- 의미: 위의 식을 만족하는 모든 파동함수는 규격화(normalized; 정규화)되었다. 즉, 입자가 이동가능 한 구역에서 입자는 무조건 어디에선가 반드시 발견된다.
- 입자의 위치를 정확하게 정하는 것은 불가능 하지만, 주어진 점 주위의 미소 영역에서 입자를 발견할 확률은 |ψ^2|로 설명할 수 있다.
보른 해석의 물리적 접근과 확장
- 파동함수는 기술하려는 계에 대한 역학적 정보를 내포한다.
- 1차원 계에 대해 파동함수의 제곱절대치는 다음과 같이 해석할 수 있다.

확률밀도에 미소 영역의 길이를 곱하면 ‘비례량’인 구역 내 입자의 존재확률 Ρ을 알 수 있다.

'고급물리학 > 현대물리학' 카테고리의 다른 글
| 【현대물리학】 복소수 (0) | 2021.12.01 |
|---|---|
| 【현대물리학】 확률밀도와 정규화 (w/ 구면극좌표) (0) | 2021.11.30 |
| 【현대물리학】 슈뢰딩거 방정식 (0) | 2021.11.30 |
| 【현대물리학】 불확정성의 원리 (0) | 2021.11.29 |
| 【현대물리학】 물질파의 이해 (w/ 전자현미경) (0) | 2021.11.28 |