Herald-Lab
【현대물리학】 슈뢰딩거 방정식 본문

슈뢰딩거 방정식

고전역학에서 입자(알갱이)와 파동은 서로 상이한 실체(entity)로 취급되었는데, 파동-입자 이중성을 실험적으로 발견하면서 고전역학의 입지가 위태로워졌다. 뿐만 아니라 대상이 작을수록 전자기 복사와 에너지의 불연속성이 매우 현저히 나타났는데, 이는 미시적 대상에 대해 연구할 때 더 이상 고전역학을 적용할 수 없음을 의미했다.
- 전제: 입자는 경로를 정하여 운동하는 것이 아니라, 파동과 같이 공간을 통해 ‘전파’된다.
- 고전역학의 궤적 개념을 대체하여 입자의 역학적 정보는 앞으로 파동함수로 나타나고, 이는 ψ로 표기한다.
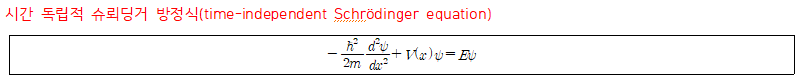
- 의미: 시간에 따라 변하지 않는 계(부피가 일정) 내부에서, 에너지 E를 가진 1차원 운동을 하는 질량 m의 알맹이의 파동함수를 구할 수 있는 방정식 ⇒ 간단한 입자의 운동에 대한 슈뢰딩거 방정식 기본형
- V(x): 위치 에서의 입자의 퍼텐셜 에너지
- ha bar=h/2π: 플랑크 상수의 변형상수로 슈뢰딩거 방정식에 자주 등장한다.
PROOF. 파동방정식과 슈뢰딩거 방정식
원래 슈뢰딩거 방정식은 뉴턴의 운동방정식과 같이 선험적인 식이다. 하지만 물리학의 역사에 근거해 입자가 파동의 성질을 갖고 있다면, 이를 지배하는 어떤 종류의 파동방정식이 존재할 것임을 유추할 수 있다.



퍼텐셜 에너지의 유형
1. 1차원에서 자유롭게 운동하는 입자의 퍼텐셜 에너지는 항상 일정하기 때문에 V(x)=V이다. ⇒ V=0로 둘 수 있다.
2. 점 x_0에서 앞뒤로 자유롭게 진동하는 입자의 퍼텐셜에너지는 (x-x_0)^2에 비례한다.
3. 거리 x만큼 떨어진 두 입자(전하의 부호를 고려하지 않은)의 퍼텐셜에너지는 다음과 같다. ⇒ V(x)=k_e(q_1q_2/x)
파동함수의 허용조건
1. 파동함수는 유한해야 한다. ⇒ 그래프가 발산하는 형태가 되면 안 된다.
2. 파동함수는 단일한 값을 가진다. ⇒ 하나의 x값에 대해 둘 이상의 같은 파동함수를 갖지 않는다.
e.g. x-를 위치 x로 y-을 파동함수 ψ로 그래프를 그릴 때 임의의 x점에 대해 수선을 그었을 때 2개 이상의 ψ값이 나오면 안 된다.
3. 파동함수는 모든 영역에 대해 연속적이다. 그래프로 파동함수가 표현될 때 끊기면 안 된다.
4. 파동함수의 1차 도함수 값 역시 연속적이어야 한다. 기울기가 연속적으로 변하는 곳이 없어야 한다!
e.g. 도함수의 그래프가 뾰족할 때, 그 점에서의 기울기가 연속적으로 변한다.
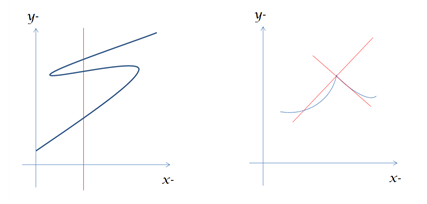
PROOF. 슈뢰딩거 방정식과 드 브로이 식
자유롭게 움직이는 입자의 경우 슈뢰딩거 식으로부터 드 브로이의 관계식이 유도될 수 있다.

한편 운동량을 통해서도 기존의 입자에 대한 운동에너지 식을 표현할 수 있다.
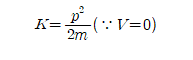
위의 두 식은 의미적으로 완전 일치하기 때문에, 드 브로이 관계식을 유도할 수 있다.

'고급물리학 > 현대물리학' 카테고리의 다른 글
| 【현대물리학】 확률밀도와 정규화 (w/ 구면극좌표) (0) | 2021.11.30 |
|---|---|
| 【현대물리학】 확률, 확률밀도, 그리고 보른의 해석 (0) | 2021.11.30 |
| 【현대물리학】 불확정성의 원리 (0) | 2021.11.29 |
| 【현대물리학】 물질파의 이해 (w/ 전자현미경) (0) | 2021.11.28 |
| [물리학-현대물리학] 광전효과 | Photoelectric Effect (0) | 2021.11.28 |





