
양자 입자 모형 Quantum Particle Model
빛과 물질이 가진 입자성과 파동성을 설명하기 위해, ‘이중성(duality of light and matter)’을 전제하는 양자입자모형(quantum particle model)을 도입했다.
1. 물체의 실체(entity)는 입자성과 파동성을 동시에 수반한다.
2. 두 가지 성질은 양자 선택성을 띤다. 빛이 물질과 상호작용하지 않을 경우 파동의 거동을 보이나, 상호작용을 하는 경우 양자화된 입자성을 보인다.
- 입자성을 가진 실체는 파동으로부터 구성될 수 있다.
파동 묶음

이상적인 파동은 단일한 주파수를 가지고 무한히 길다. 그러므로 입자를 파동과 구별 짓는 가장 큰 특징은 공간의 국소성이다.
- 무한히 긴 파동으로부터 위치가 국소적인 실체
- 파동 1: x=0에서 마루를 가진 파동
- 파동 2: 파동 1과 최고 진폭은 같으나 주파수가 다른 파동 ⇒ x=0에서 역시 같은 마루를 가진다.

파동 1과 파동 2는 중첩의 결과 파동이 일치하는 위상과 일치하지 않는 위상이 교대로 나타난다. ⇒ 맥놀이
- 맥놀이가 진행되는 경우 중첩된 부분의 공간적 국소성이 발생한다. ⇒ 보강간섭이 일어나는 공간영역과 상쇄간섭이 일어나는 공간영역 간의 차이가 파동 전체의 공간적 국소성과 같다!
각기 다른 주파수를 가진 새로운 파동을 계속 더하는 경우 다음과 같은 특징이 나타난다.
- 각각의 새로운 파동의 최고점은 모두 x=0에 위치하도록 설정한다. 그러나 각각의 파동의 주파수가 다르므로 이후 지점의 파동진폭은 보강이 되거나 혹은 상쇄가 된다.
- 수많은 파동을 고려하면 임의의 한 점에서 파동함수의 양의 값 확률은 음의 값 확률과 같고, 모든 마루가 중첩된 x=0 근방을 제외한 모든 점에서 상쇄간섭이 발생한다.
파동 묶음(wave packet): 보강간섭이 일어난 미소 영역 ⇒ x=0 근방의 공간적 국소영역으로 공간의 국소성 설명에 적합하다.
- 파동묶음 이외의 중첩결과는 0이다.
- 파동묶음은 공간적 국소성으로 입자로 간주할 수 있고, 묶음의 위치가 곧 입자의 위치이다.
PROOF. 파동 묶음의 수학적 표현
두 파동의 진폭은 같으나 서로 다른 주파수를 가진다.

두 파동이 중첩되면 다음과 같다.


두 번째 코사인 함수 인자는 각 파동에 대한 평균값과 일치하는 파수와 주파수를 가진 파동을 표현했다.


- 포락선[그림 3]은 각각의 파동과는 다른 속력으로 공간을 움직인다.
- 가능한 극단적 예로 반대 방향으로 움직이는 두 파동을 조합이 있다. ⇒ 두 파동이 같은 속력으로 움직일 때, 정상파를 구성하기 때문에 포락선의 속력은 0이다.

- 의미: 파동의 위상속력은 파동 식에서 공간 변수의 계수와 시간 변수의 계수 비와 같다.
위의 논리를 따라, 포락선 함수 역시 파동의 형태이므로 ‘군 속력(group speed)’을 정의할 수 있다.

두 파동이 아닌 아주 많은 파동의 중첩에 대해 군 속력과 비율은 미분을 취할 수 있다.


- 의미: 무수히 많은 파동이 중첩되었을 때 형성한 포락선(파동 군)이 가지는 속력
군 속력의 분자와 분모 각각에 ha bar=ha/2π(플랑크 상수 변환 값)를 곱한다.

마지막으로 중첩된 파동에서의 포락선이 입자를 나타낼 가능성은 다음과 같이 정리할 수 있다.

위의 식을 운동량에 대해 미분하면 다음과 같다.
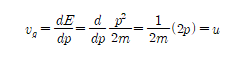
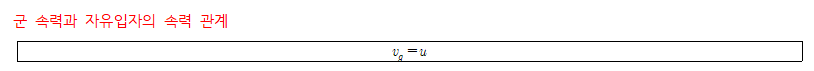

불확정성의 원리


- 의미: 입자의 정확한 위치와 운동량을 동시에 측정하는 것이 불가능하다.
- 1927년, 독일의 이론물리학자 하이젠베르크(Werner Heisenberg, 1901~1976)가 제안했다.
- 실험과정에서 일어나는 실수나 기계가 가진 한계에 의한 오차범위가 아니다! ⇒ 물질의 양자적 구조 때문에 발생하는 ‘불가피한(inevitable)’ 오차
- 운동량의 불확정성의 곱은 항상 어떤 최솟값보다 크고 이는 플랑크 상수의 변환 값(변환 식) ha bar의 절반 크기이다.
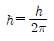
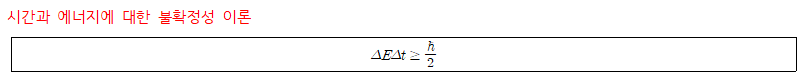
- 의미: 에너지 보존이 극도의 짧은 시간 동안 ΔE만큼 위배될 수 있다.
'고급물리학 > 현대물리학' 카테고리의 다른 글
| 【현대물리학】 확률밀도와 정규화 (w/ 구면극좌표) (0) | 2021.11.30 |
|---|---|
| 【현대물리학】 확률, 확률밀도, 그리고 보른의 해석 (0) | 2021.11.30 |
| 【현대물리학】 슈뢰딩거 방정식 (0) | 2021.11.30 |
| 【현대물리학】 물질파의 이해 (w/ 전자현미경) (0) | 2021.11.28 |
| [물리학-현대물리학] 광전효과 | Photoelectric Effect (0) | 2021.11.28 |
