확률밀도
정규화된 파동함수를 얻으면 확률밀도를 결정할 수 있다.
PROOF. 1차원 자유운동을 하는 입자 파동함수
슈뢰딩거 방정식에 대한 해를 확인하기 위해서 다음 전제를 따른다. ⇒ 파동함수와 에너지 항을 슈뢰딩거 방정식에 대입하여 값이 일치하는 지 확인한다.
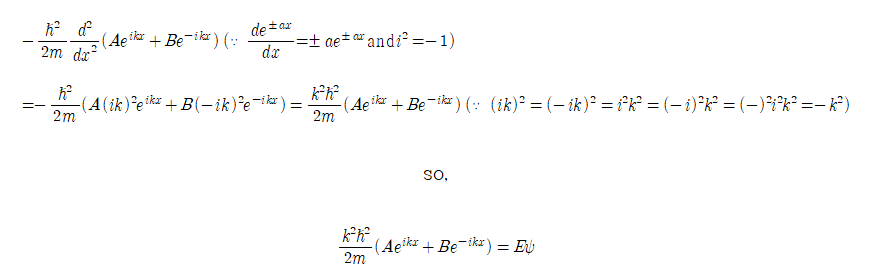
1. 만약 B=0이라면 파동함수의 해가 매우 간단해진다.
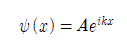
이들에 대한 확률밀도는 다음과 같이 구한다.
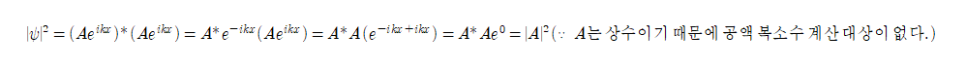
- 위의 확률밀도는 에 무관하다! ⇒ x-상의 어디에서나 입자를 발견할 확률이 동일하다. 이는
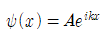
식으로 입자의 파동함수가 주어지면, 입자의 발견을 전혀 예측할 수 없음을 의미한다!
2. 마찬가지로 A=0일 때, 파동함수의 해에 대한 확률밀도는 |B|^2이다.
3. A=B
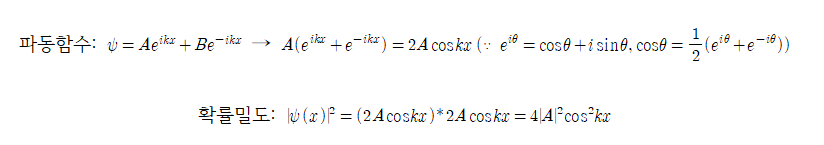
- 의미: 확률밀도는 입자가 발견될 확률과 비례하는 분포로 진폭이 클수록 발견확률이 높다. 위의 식은 0과 4|A|^2사이에서 주기적으로 변하는 파동모양을 가진다.
- 마디(node): 확률밀도가 0이 되는 지점 파동함수가 0을 통과하는 지점으로 마디에서는 파동함수가 발견되지 않는다.
- 의미: 무한소가 아닌 특정한 영역(x_1에서 x_2까지)에서 ‘계’를 발견할 확률은 확률밀도를 대상 공간 영역에 걸쳐 적분한 값과 같다.
- 식에서 확률밀도는 정규화된 파동함수의 제곱이다.
- 파동함수가 정규화 되었을 때 그 제곱의 적분은 역시 1이 되어야 한다.
PROOF. 전자를 발견할 확률의 계산
탄소 나노 튜브(carbon nano-tube)[그림 1]의 최소 에너지 전자들에 대한 정규화 파동함수가 다음과 같다.
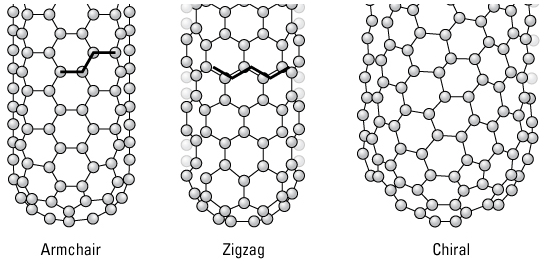
0.4 ⇒ 주어진 탄소 나노튜브 사이에서 전자를 발견할 확률은 약 40%이다.
정규화 Normalization
만약 파동함수가 슈뢰딩거 식의 한 해면 여기에 임의의 상수 N을 곱한 Nψ도 또한 해가 된다. ⇒ 시간에 무관한 슈뢰딩거 방정식의 모든 항에 파동함수 ψ가 들어있어 어떤 상수인자든지 모두 상쇄될 수 있기 때문이다.
- 파동함수를 임의의 상수 인자만큼 변화시킬 수 있는 것은 언제나 정규화 상수 N을 구할 수 있고, 그 결과 보른 해석에서의 비례관계를 항상 등식으로 바꾸어 줄 수 있음을 의미한다.
PROOF. 정규화 상수 구하기
따라서 위의 적분을 구하면 정규화 상수 N을 구할 수 있고, 파동함수를 ‘정규화’시킬 수 있다!
- 특별한 언급이 없는 한은 언제나 1로 정규화된 파동함수를 사용한다.
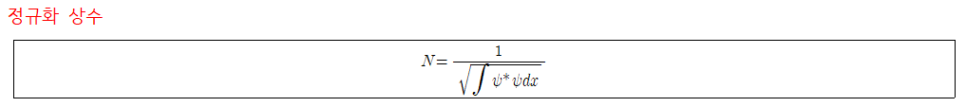
정규화 적분
정규화를 시키는 대상이 놓인 공간에 따라 1로 정규화된 적분 식을 각각 세울 수 있다. 아래 파동함수는 모두 정규화 되어있다.
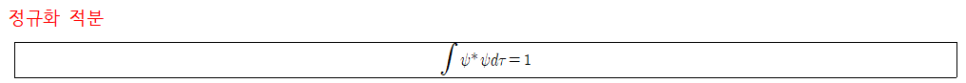
- dτ는 차원에 따라 다른 값을 가진다.
·1차원: dx
·3차원: dxdydz
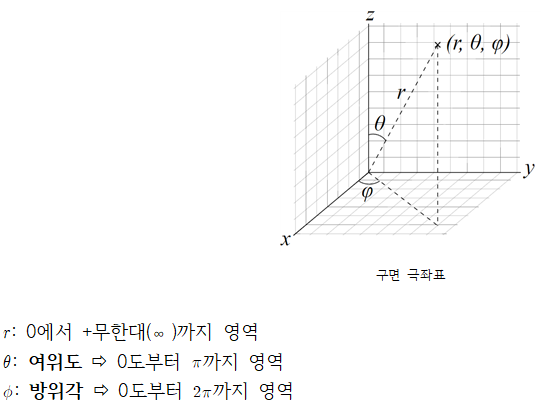
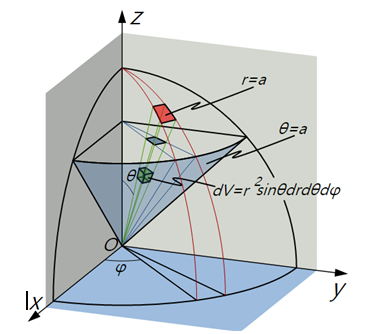
구면극좌표
구 대칭을 갖는 계를 분석하는 데 있어 구면좌표계가 가장 널리 알려져 있다.
'고급물리학 > 현대물리학' 카테고리의 다른 글
| [물리학-현대물리학] 이온결합 | Ionic Bonding (0) | 2023.11.02 |
|---|---|
| 【현대물리학】 복소수 (0) | 2021.12.01 |
| 【현대물리학】 확률, 확률밀도, 그리고 보른의 해석 (0) | 2021.11.30 |
| 【현대물리학】 슈뢰딩거 방정식 (0) | 2021.11.30 |
| 【현대물리학】 불확정성의 원리 (0) | 2021.11.29 |