Herald-Lab
[물리학-전자기학] 30. 전자기학을 위한 벡터해석 (1) - 벡터 대수 본문

벡터 대수
스칼라(scalar): 크기로 규정되는 양으로 전자기학에서 스칼라량은 대표적으로 전하와 전압이 있다.
벡터(vector): 크기와 함께 방향 또한 함께 고려해야 하는 양으로 전자기학에서 벡터량은 대표적으로 전기장, 자기장이 있다.
- 벡터는 기하학적으로 방향을 나타내는 선분인 화살표[그림 1]로 나타난다.
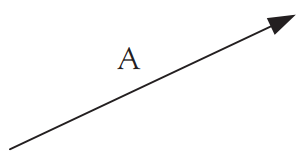
- 벡터의 방향은 화살표의 머리이다. 한편 크기는 화살표의 길이와 같다.
- 벡터의 위치만 옮기는 평행이동의 경우, 벡터량은 달라지지 않는다.
벡터 덧셈
두 벡터의 덧셈 A+B는 기하학적으로 A의 머리에 B의 꼬리를 붙이는 방식[그림 2]으로 구할 수 있다.

혹은 [그림 3]과 같이 평행사변형법을 사용해도 된다.
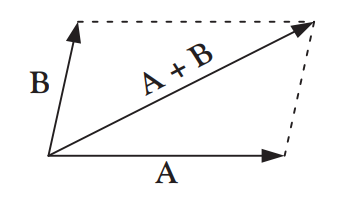
두 가지의 두 벡터의 덧셈법은 그 결과가 서로 일치한다.
- 벡터의 덧셈은 교환법칙(commutative)과 결합법칙(associative)이 성립한다.

스칼라 곱셈
- 어떤 벡터에 스칼라량 a를 곱하면 그 벡터의 크기는 a배가 된다.
- a>0인 실수이면, 그 벡터의 방향은 바뀌지 않는다. 하지만 반대의 경우(a<0)인 경우, 그 벡터의 방향은 바뀐다.
- 스칼라 곱셈(multiplication of a vector by a scalar, scalar multiplication)은 분배법칙(distributive)이 성립한다.

4. 어떤 벡터를 스칼라 나눗셈 함은 그 벡터에 스칼라량 a의 역수 1/a를 곱하는 것과 같다.
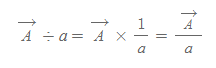
특히 4번의 성질을 이용하여, 벡터 A를 자신의 크기 A로 나누면 길이가 1이면서 방향은 A와 같은 벡터가 결과 값으로 나타나는 데, 이를 단위 벡터(unit vector)라 정의한다.
Unit Vector
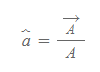
■
- 단위벡터의 크기는 1이다.
- 단위벡터의 방향은 그 벡터 A의 방향과 같다.
스칼라곱과 벡터곱
벡터를 곱하는 방법은 크게 두 가지 종류가 있다.
- 스칼라곱(scalar product): 점곱(dot product), 벡터 A에 대한 벡터 B의 사영[그림 4]을 곱한 값으로 결과는 스칼라량이다.

점곱은 다음과 같이 정의 된다.
Scalar Product(Dot Product)

■
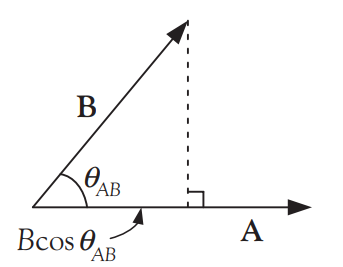
기하학적으로 점곱 AB는 벡터 A의 크기에 벡터 B의 벡터 A 방향성분 Bcosθ을 곱한 것과 같다.
- θ이 0도에서 90도 사이인 경우 cosθ는 양수이고, 따라서 점곱은 양의 값을 갖는다.
- θ이 90도에서 180도 사이인 경우 cosθ는 음수이고, 따라서 점곱은 음의 값을 갖는다.
- θ이 90인 경우 cos90=0이므로, 점곱은 0이 된다. ⇒ 수직인 두 벡터의 dot product는 언제나 0이다.
점곱의 성질
- 점곱은 교환법칙이 성립한다.
- 점곱은 분배법칙이 성립한다.
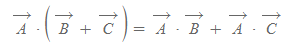
단위벡터의 점곱

3차원 상에서 단위벡터는 [그림 6]과 같이 나타나며 이들을 서로 스칼라곱한 결과는 다음과 같다.
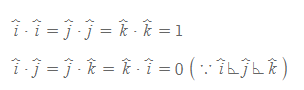
- 단위벡터의 스칼라곱에서 윗 내용은 사잇각 θ이 0인 것으로 서로 평행하는 경우 scalar product의 결과는 다음과 같다.

단, 단위벡터의 크기는 1이므로 1을 제곱해도 역시 1이 나오기 때문에 위와 같은 결과가 성립된다.
- 단위벡터의 스칼라곱에서 아래 내용은 사잇각 θ이 90인 것과 정확히 일치한다.
2. 벡터곱(vector product): 가위곱(cross product), 벡터 A, B를 가위곱하면 그 결과 값은 벡터량이다.

Vector Product(Cross Product)
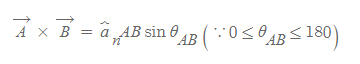
■

vector product 식의 물리량은 [그림 8]을 통해 확인할 수 있다.
- 벡터 A, B의 cross product 크기는 ABsinθ_AB이다. 즉, 벡터 A와 B가 만드는 평행사변형의 면적과 정확히 일치한다.
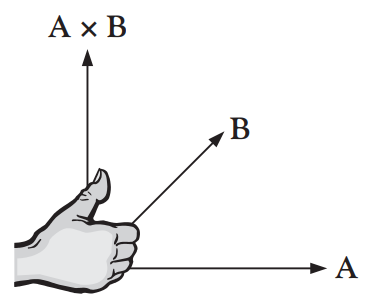
- 단위벡터 a_n은 가위곱의 방향으로 평행사변형이 놓인 평면에 수직한다. a_n의 방향은 [그림 9]와 같이 오른손 규칙으로도 확인할 수 있다.
가위곱의 성질
- 가위곱은 분배법칙이 성립한다.
- 가위곱은 교환법칙이 성립하지 않는다. 대신 역교환법칙을 따른다.
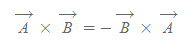
3. 가위곱을 하는 두 벡터 A, B의 사잇각이 90도일 때, sin90=1이므로 최대 크기 AB를 갖는다. 반면 두 벡터 A, B의 사잇각이 0도일 때, sin0=0이므로 벡터곱의 크기 또한 0이 된다.
단위벡터의 가위곱
단위벡터의 가위곱은 가위곱의 성질에 따라 다음과 같이 정리된다.
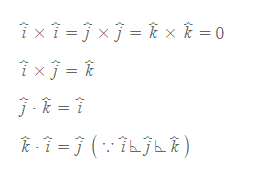
삼중곱 Triple Product
삼중곱은 두 벡터의 곱과 마찬가지로 그 결과에 따라 2가지 곱이 존재한다.
- 스칼라삼중곱
- 벡터삼중곱
스칼라삼중곱

스칼라삼중곱의 결과는 스칼라량으로, 세 벡터가 만드는 평행육면체의 부피와 그 값이 같다.
- 단위벡터 a_n은 벡터 B와 C의 가위곱 방향과 같다. 또한, Base_CB는 벡터 B, C의 가위곱 면적이다.
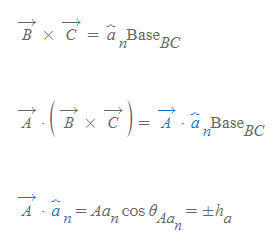
- 만약 벡터 A와 단위벡터 a_n의 사잇각이 90도 미만이면 [그림 10]의 h_a 값은 양수이다. 반면 90도를 초과한다면 h_a 값은 음수이다.
- 벡터 A와 단위벡터 a_n의 스칼라곱의 결과는 평행육면체의 높이 값과 같다. 그리고 이 평행육면체의 부피가 스칼라삼중곱이다.
스칼라삼중곱

■
- 스칼라삼중곱의 점곱, 가위곱 순서를 바꾸어도 결과는 동일하다.

벡터삼중곱
벡터삼중곱은 간단하게 결과 값만 확인하자.
벡터삼중곱
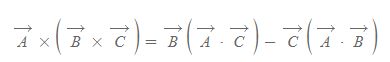
■
'물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 34. 전기장 (1) | Electric Field (1) (0) | 2023.09.20 |
|---|---|
| [물리학-전자기학] 35. 전기장 (2) | Electric Field (2) (0) | 2023.09.20 |
| [물리학-전자기학] 33. 쿨롱의 법칙 | Coulomb's Law (0) | 2023.09.18 |
| [물리학-전자기학] 32. 전하, 대전, 유도 | Electric Charges, Electrification, and Induction (0) | 2023.09.17 |
| [물리학-전자기학] 31. 전자기학을 위한 벡터해석 (2) - 좌표계와 그 변환 (0) | 2023.09.03 |





