
쿨롱의 법칙
Coulomb's Law

프랑스의 물리학자인 쿨롱(Charles-Augustin Coulomb, 1736~1806)은 자신이 발명한 비틀림 저울(torsion balance)[그림 1]을 활용하여 대전된 물체 사이의 전기력의 '크기'를 측정하였다.

- 원리: 대전된 두 구 사이에는 전기력이 작용한다. → 전기력에 의해 두 구는 서로 잡아당기거나 혹은 밀어낸다. → 파란 색 대전 구를 매단 줄이 비틀어진다. → 비틀어진 줄의 복원력 토크는 줄의 회전한 각도에 비례한다.
- 마찰된 대전 구 사이의 전기력은 (질량에 의한) 만유인력에 비해 대단히 큰 값이다. ⇒ 만유인력에 의한 인력 효과는 충분히 무시할 수 있다.

쿨롱의 법칙(쿨롱 법칙) [그림 2]

■
- 물리량
- q: 부피가 없는 대전 입자로 점전하로 가정한다.
- k_e: 쿨롱 상수, 대략적인 크기는 9.00×10^9[Nm^2/C^2]이다.
- r: 두 전하 사이의 거리
- 단위: 쿨롱의 법칙은 전기력의 크기를 나타내므로, 힘의 단위인 뉴턴 단위로 표기한다.
- 전기력은 보존력이며 보존장의 특성을 가진다.
1[C] 전하는 근사적으로 6.242×10^18개의 전자 또는 양성자 수에 해당하는 매우 큰 값의 전하량이다. ⇒ 그러므로 문제에서는 주로 마이크로쿨롱 단위[μC]를 쓴다.
쿨롱상수

■
- 물리량
- ε_0: 자유공간의 유전율(진공유전율, 전매상수, permittivity of free space), 전하 사이에 전기장이 작용할 때, 그 전하 사이의 매질이 전기장에 미치는 영향을 나타내는 물리적 단위)
- 쿨롱상수는 진공 중(in vacuum)에서 상수이다.
- 만약 특정한 매질의 유전율 ε을 대입할 경우, 외부 전기장을 유전체에 가했을 때 일어난 유전 분극 현상으로 (유전상수)×(진공유전율)로 계산한다.
유전율의 3가지 의미
- 물질의 전극분극 용이성: 외부 전기장에 의한 전하의 전기분극으로 전기쌍극자의 형성이 어느 정도 일어나는 가를 확인할 수 있다.
- 물질이 전하를 저장할 수 있는 능력으로, 외부 전기장에 의한 전기분극으로 전하가 축전되는 효과를 확인할 수 있다.
- 유전체 또는 부도체의 성질을 나타내는 값으로 속박전하만 존재한다.
즉, 유전율이 클수록 (1)더 많은 전하를 저장할 수 있고, (2)전자기파의 매질 손실이 적으며, (3)같은 주파수에서 전자회로를 더 작게 만들 수 있다.
유전율은 특정 공간의 상수(constant)로 진공에서는 다음과 같이 그 값이 알려져 있다.


쿨롱의 법칙에 의해 계산되는 전기력의 방향은 [그림 3]과 같이 두 전하의 극성에 따라 결정된다. 쿨롱의 법칙 대입 결과 (-)값을 가지면 두 전하는 서로를 당기는 방향으로, (+)값을 가지면 두 전하는 서로 멀어지는 방향으로 힘의 방향성이 결정된다.
전기력은 또한 힘의 일종이므로 뉴턴의 운동 제3법칙을 따른다.
다점전하계
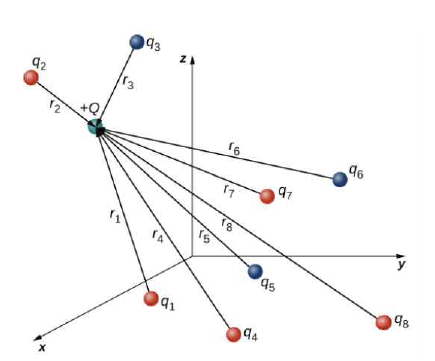
그림 4. 다전하계 [출처: University Physics Volume 2, Openstax, 2nd ed.]
[그림 4]처럼 두 개 이상의 점전하가 모인 계를 다점전하계라 하며, 만약 삼차원 상에 입자 2, 3, 4가 입자 1에 전기력을 작용한다면 합력은 다음과 같이 계산한다.
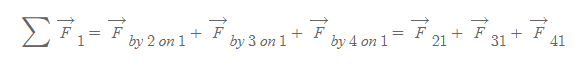
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 34. 전기장 (1) | Electric Field (1) (0) | 2023.09.20 |
|---|---|
| [물리학-전자기학] 35. 전기장 (2) | Electric Field (2) (0) | 2023.09.20 |
| [물리학-전자기학] 32. 전하, 대전, 유도 | Electric Charges, Electrification, and Induction (0) | 2023.09.17 |
| [물리학-전자기학] 31. 전자기학을 위한 벡터해석 (2) - 좌표계와 그 변환 (0) | 2023.09.03 |
| [물리학-전자기학] 30. 전자기학을 위한 벡터해석 (1) - 벡터 대수 (0) | 2023.09.03 |