단위벡터와 벡터 성분
Unit Vectors and Components
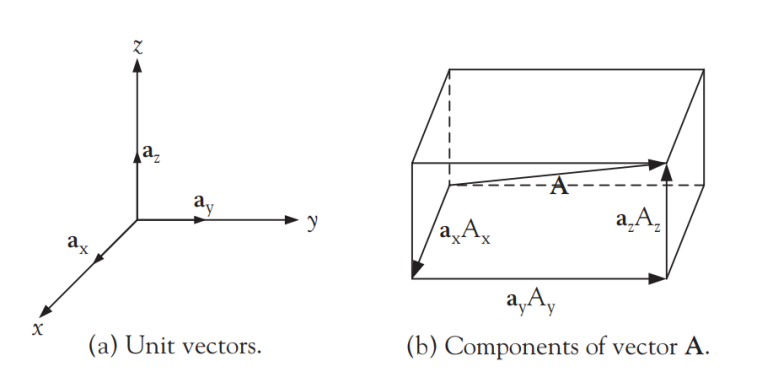
좌표계를 도입하면 벡터를 성분(components)으로 나타낼 수 있고, [그림 1]은 직각 좌표계(rectangular coordinate system, Cartesian coordinate system)를 사용하여 나타낸 벡터 그림이다.
- [그림 1]의 (a)는 unit vector들로 직각 좌표계의 x, y, z축과 그 방향성이 정확히 일치한다.
- [그림 1]의 (b)는 임의의 벡터 A로 x, y, z축에 각각 투영시킨 정사영벡터(projections)가 함께 그려져 있다. ⇒ 벡터 덧셈에 따라 벡터 A는 projection을 활용하여 아래와 같이 정의된다.
- 성분벡터 Vs. 성분
3차원 직각 좌표계에서 벡터 A의 성분벡터와 성분은 아래와 같이 정의된다.
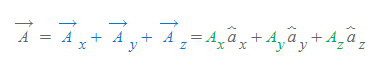
- 파란색은 (벡터 A의) 성분벡터이고, 초록색은 (벡터 A의) 성분이라 한다.
세 가지 좌표계
Three Geometry Coordinate System
전자기학에서 다루는 문제는 3차원의 세상이고, 이를 표현할 수 있는 좌표계는 크게 3가지이다.
- 직각좌표계(rectangular coordinate system)
- 원통좌표계(cylindrical coordinate system)
- 구좌표계(spherical coordinate system)
직각좌표계
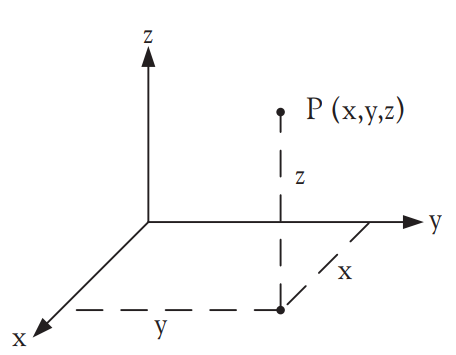
직각좌표계는 오른손 법칙[그림 3]으로 설정된 좌표축의 시스템이다.
- 각각의 축은 x, y, z로 명명되며, 이들의 단위벡터는 i, j, k 또는 hat x, hat y, hat z로 표현한다.
- 원점으로부터 각 축을 향해 뻗어나가는 정도를 x, y, z라고 하면, 점 P는 P(x, y, z)[그림 2]로 표현된다.
원통좌표계
- 원통좌표계는 직각좌표계의 x, y, z처럼 세 가지의 특수한 좌표값을 갖는다.
- ρ: (점 P가) z축으로부터 떨어진 거리[그림 4]
- φ: 방위각(azimuth angle), +x축으로부터 반시계 방향의 각도
- z: xy평면으로부터 높이
- 각각의 좌표는 아래와 같은 특수한 조건값을 만족해야 한다.
원통좌표계의 각각의 좌표에 대한 단위벡터는 다음과 같다.
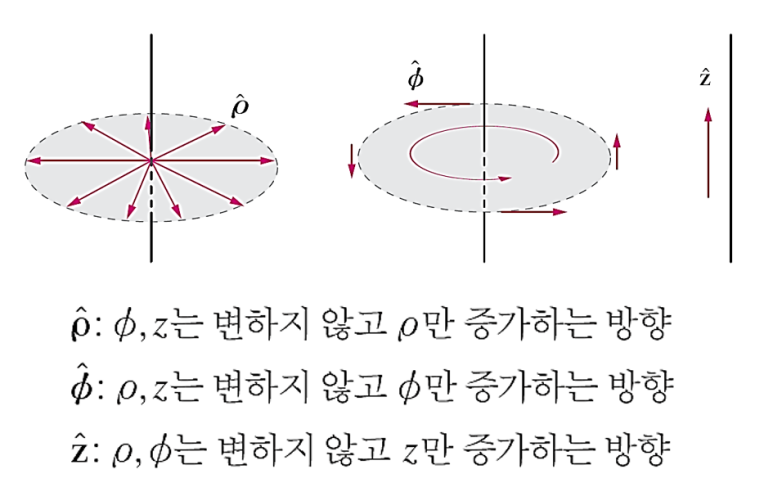
원통좌표계의 단위벡터는 방사(ρ), 회전(φ), 그리고 증가(z)의 형태를 보인다.
그림 6
- 원통좌표계의 각 단위벡터는 [그림 6]과 같이 서로 수직한다. 특히 단위벡터 ρ와 φ는 φ좌표의 함수이다.
- 원통좌표계의 기본단위벡터를 활용하여, 각 성분의 크기를 가진 벡터를 아래와 같이 표현할 수 있다.
직각좌표계와 원통좌표계의 변환
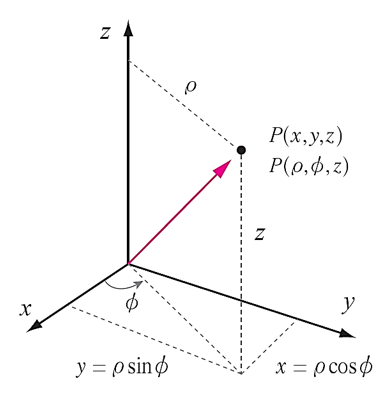
그림 7
3차원의 좌표 시스템에 놓인 점 P는 직각 좌표계와 원통 좌표계 모두의 좌표값으로 표현될 수 있으며, 이들은 서로 변환되어 계산될 수 있다.
- 원통 → 직각: 원통좌표를 이용하여 직각좌표를 구하는 식
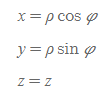
- 직각 → 원통: 직각좌표를 이용하여 원통좌표를 구하는 식
구좌표계
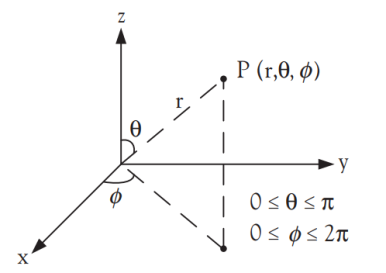
- 구 좌표계 역시 특수한 세 가지 좌표를 갖는다.
- r: 원점으로부터 떨어진 거리
- θ: 편각(polar angle), +z축으로부터의 각도(z축과 선 OP가 이루는 각도[그림 8])
- φ: +x축으로부터 반시계 방향의 각도
- 각각의 좌표는 아래와 같은 특수한 조건값을 만족해야 한다.
구좌표계의 기본단위벡터는 [그림 9]와 같은 형태를 갖는다.
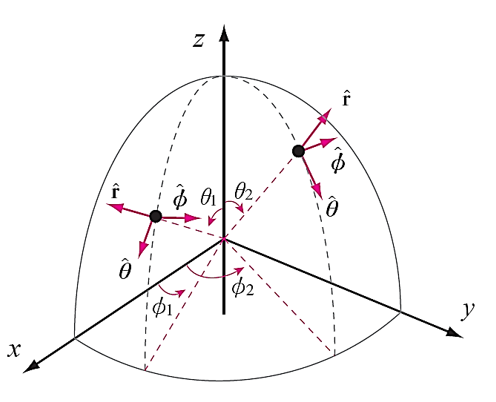
- 구좌표계의 기본단위벡터를 활용하여, 각 성분의 크기를 가진 벡터를 아래와 같이 표현할 수 있다.
직각좌표계와 구좌표계의 변환
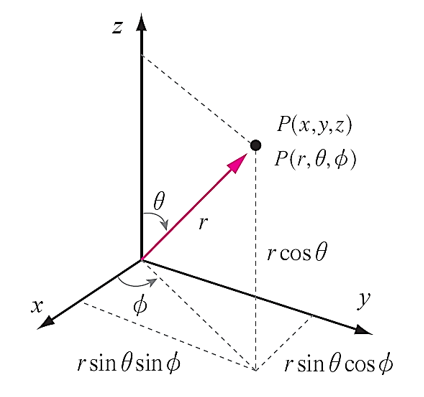
그림 10
직각좌표계를 구좌표계 또는 반대의 좌표 내용으로 변환할 수 있다.
- 구좌표 → 직각좌표: 구좌표를 활용하여 직각좌표를 구하는 식
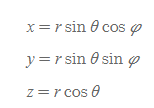
- 직각좌표 → 구좌표: 직각좌표를 이용하여 구좌표를 구하는 식
원통좌표-구좌표의 직접적인 변환은 그 공식이 비직관적이기 때문에, 대부분 처음 제시된 좌표계의 좌표를 직각좌표로 변환한 뒤 이 변환된 직각좌표를 원통좌표 또는 구좌표로 변환한다.
좌표의 변환
Equations of Transformation Between Coordinate Systems
좌표의 변환식을 정리하면 아래와 같다.
1. 원통좌표를 이용하여 직각좌표를 구함 식
2. 직각좌표를 이용하여 원통좌표를 구함 식
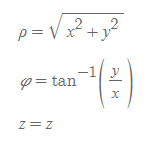
- 원통좌표와 직각좌표의 z값은 서로 같다.
- 원통좌표의 ρ는 점 P의 xy평면(2차원) 위의 투영과 원점 사이의 거리이고, 방위각 φ 또한 xy평면(2차원) 상의 각이므로, 둘은 '2차원 상의' 직각좌표와 평면 극좌표(polar coordinate) 간의 관계식과 매우 유사하다.
3. 구좌표를 활용하여 직각좌표를 구함 식
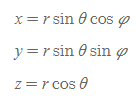
4. 직각좌표를 이용하여 구좌표를 구함 식
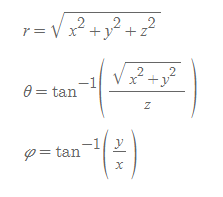
이제 이를 활용해 각 좌표계의 위치벡터 표현을 알아보도록 하자.
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 34. 전기장 (1) | Electric Field (1) (0) | 2023.09.20 |
|---|---|
| [물리학-전자기학] 35. 전기장 (2) | Electric Field (2) (0) | 2023.09.20 |
| [물리학-전자기학] 33. 쿨롱의 법칙 | Coulomb's Law (0) | 2023.09.18 |
| [물리학-전자기학] 32. 전하, 대전, 유도 | Electric Charges, Electrification, and Induction (0) | 2023.09.17 |
| [물리학-전자기학] 30. 전자기학을 위한 벡터해석 (1) - 벡터 대수 (0) | 2023.09.03 |