[물리학-전자기학] 35. 전기장 (2) | Electric Field (2)

 

전기선속

Flux of Electric Field Intensity

 

그림 1. 전기력선이 통과하는 가상의 면 [출처: University Physics Volume 2, OpenStax, 2016, p.215]

 

 

전기선속(전기다발, flux of electric field intensity): 전기력선 다발 또는 집합

• 전기선속은 어떤 면을 통과하는 전기력선의 개수에 비례한다.
• 전기선속 내 실질적인 전기력선의 개수를 기호로 φ_E라 쓴다.
• 전기선속과 전기선속에 수직한 면의 면적[그림 1]을 통해 전기장 크기를 아래와 같은 수식으로 작성할 수 있다.

​

전기장 크기

 

■

​

• 물리량

1. φ_E: 전기력선의 개수
2. A_⊥: 전기력선에 수직한 면의 면적

​

• 전기장이 강한 영역에서 전기력선은 높은 밀도를 갖는다.

​

전기장 크기 식을 통해 전기선속의 공식을 또한 쉽게 유도할 수 있다.

​

전기선속

 

■

• 의미: 전기선속은 전기장의 크기와 전기력선이 지나간 전체 면적에 비례한다.
• 전기장의 방향과 표면적에 수직하는 경우에만 성립하는 공식으로 수직하지 않는 경우의 전기선속 φ는 둘의 방향이 완전 수직한 φ_E에 비해 그 값이 작다.

​​

 

그림 2. 면과 수직한 단위벡터

 

 

그림 3. 단위면적을 지나는 전기선속 [출처: University Physics Volume 2, OpenStax, 2016, p.247]

 

면과 수직한 단위벡터

면(파란색, 면 A)과 수직한 법선을 긋고 이를 단위벡터 hat n으로 잡으면 [그림 2]과 같이 나타난다. 만약 전기장 벡터 E와는 수직하지 않지만, 비스듬한 각도 θ를 두고 [그림 3]과 같이 면(파란색, 면 B)을 잡았을 때, 새롭게 그은 법선과 평행한 단위벡터 hat n_2를 표현할 수 있다.

​

이들 둘의 관계는 다음과 같은 식으로 나타난다.

• hat n_1: 전기장 벡터에 대해 완전 수직한 면에 대해 수직한 단위벡터
• hat n_2: 전기장 벡터에 대해 θ만큼 기울기를 같은 면(면 B)에 대해 수직한 단위벡터
• θ: 면 B가 균일한 전기장의 방향에 대해 이루는 각도

​

hat n_1과 hat n_2는 수학적으로 면에 대한 벡터(면벡터, area vector)로 분류된다.

• 단, 가우스 법칙에 대해서 면벡터는 단순히 면에 대한 법선(면법선)으로 봐도 무방하다.

​

전기선속의 크기

전기선속의 크기는 아래와 같이 정리할 수 있다.

1. 면에 대한 법선이 전기장의 방향과 평행일 때 전기 선속의 크기는 최댓값을 갖는다.
2. 면에 대한 법선이 전기장의 방향과 수직일 때 전기 선속의 크기는 0이다. ⇒ 알짜 전기선속이 0이다.

​

일정한 크기의 전기장 조건에서 전기 선속

전기장이 균일하지 않은 경우, 전기장은 넓은 면에 걸쳐 변할 수 있으므로, 주어진 선속에 대한 앞선 정의는 미소 넓이 요소에 한정된다.

• ΔA: 방향을 고려하지 않은 미소 넓이의 크기
• Δ벡터A_i: 법선의 방향을 고려한 i번째 요소의 넓이

​

미소 넓이의 전기 선속

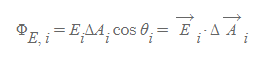
• 전기장과 표면적의 법선벡터[그림 4]는 모두 벡터량이고 코사인 항이 또한 존재하므로 둘을 스칼라곱으로 표현할 수 있다.

​

표면을 통과하는 전체 선속의 근삿값은 모든 요소에 대한 선속을 합하여 얻을 수 있고, 만약 각 요소의 넓이를 0에 근접하게 만든다면, 요소의 수는 무한히 많아지며 그 합은 적분으로 대신 표현할 수 있다.

​

전기장이 균일하지 않은 곳에서 전기 선속

■

​

• 의미: 선속의 값은 전기장의 형태와 표면에 의해 결정된다.

 

그림 4. 전기장과 법선의 관계 [출처: University Physics Volume 2, OpenStax, 2016, p.250]

 

​

전기력선 그리기

전하로부터 뻗어나가는 전기력선은 크게 ‘3가지의 그리기 규약’을 만족해야 한다.

1. 전기력선은 양전하에서 시작해 음전하로 끝난다. ⇒ 전기력선에 그려진 화살표의 방향은 양의 전하'로부터는' 뻗어나가는 방향을, 음의 전하'로는' 들어가는 방향성을 갖는다.
2. 전기력선의 수는 전하의 크기에 비례한다.
3. 두 전기력선은 서로 교차할 수 없다.