
연속전하분포
Continuous Charge Distribution
연속전하분포(continuous charge distribution): 수많은 전하 사이의 거리가 전기장을 구하고자 하는 점(P)까지의 거리에 비해 매우 가까운 경우의 연속적인 전하체
- Δq: 전하체의 작은 전하요소(미소전하요소, charge element)
미소전하요소에 의한 전기장
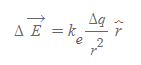
미소전하요소가 모인 전하체의 총 전기장은 시그마 기호(∑)를 이용해 다음과 같이 표현할 수 있다.
전하체의 전체 전기장
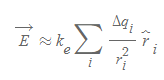
전하분포가 연속적이므로 Δq_i→0인 극한에서 P의 전기장은 다음과 같이 계산된다.
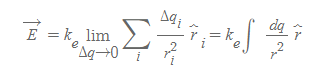
연속전하분포의 전기장
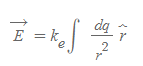
■
- 의미: 연속전하분포의 총 전기장으로, 적분구간은 전체 전하분포영역이다.
전하는 (1)선, (2)면 및 (3)부피에 분포할 수 있으므로, 전하밀도(charge density)[그림 1]의 개념을 사용하는 것이 편하다.
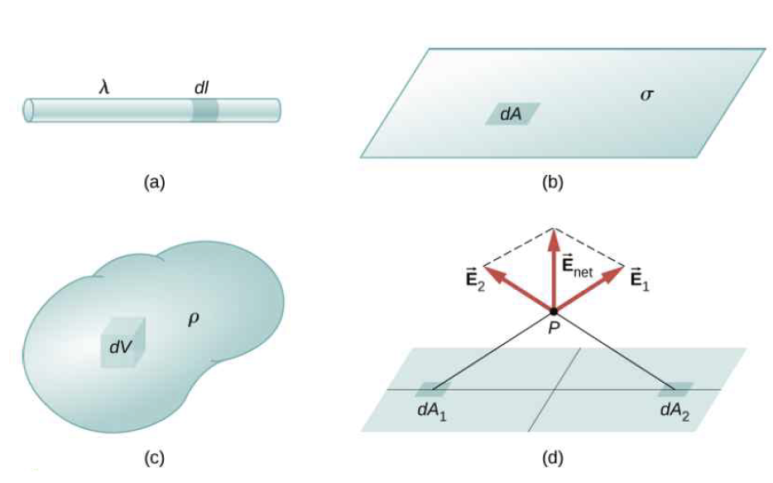
- (a): λ, 선전하밀도
- (b): σ, 면전하밀도
- (c): ρ, 부피전하밀도
밀도의 공식 (질량)/(부피)를 응용하여 전하밀도는 (전하)/(부피)도 계산되며, 각 전하밀도는 그리스 기호로 lambda(λ), sigma(σ), rho(ρ)로 표현된다.
부피전하밀도
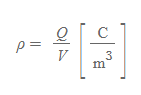
표면전하밀도
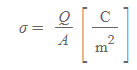
선전하밀도
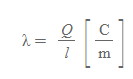
전하가 부피, 면 혹은 선에 따라 균일하게 분포하지 않은 경우, 미소 전하량은 다음과 같이 정리할 수 있다.

가우스 법칙
Gauss's Law
닫힌곡면에서의 선속
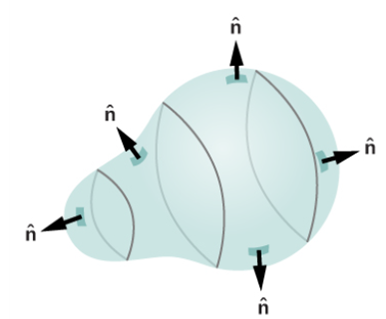
닫힌곡면(가우스 면, 가우스 곡면, closed surface, Gauss's surface): 내부공간과 외부공간을 완벽히 분리하고, 이 면을 지나지 않고서는 한 공간에서 다른 공간으로 이동할 수 없는 표면[그림 2]
알짜 전기력선 수란, 표면을 통과하여 나가는 전기력선 수에 표면을 통과하여 들어오는 전기력선 수를 뺀 값이다.
- 양의 선속: 나가는 전기력선 수 들어오는 전기력선 수
- 음의 선속: 나가는 전기력선 수 들어오는 전기력선 수
닫힌곡면의 전기선속
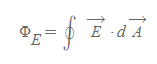
■
- 물리량
- ∮: 적분하려는 면이 닫혀있음(닫힌곡면)을 의미
- E: 전기장
- dA: 미소면적(가우스 면)
- 의미: 전기장의 크기를 계산할 시, 표면에 수직한 전기장 성분만을 고려한다.
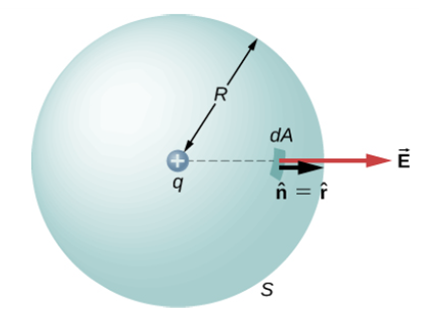
[그림 3]과 같이 가우스 면을 지나는 알짜 전기 선속과 닫힌곡면 내의 양전하 사이의 관계를 알아보자.
가우스 곡면이 구를 이루는 경우, 전기장의 크기는 구면에 대해 어디든지 같다. 그리고 구면 내의 양전하는 방사형태로 전기력선을 '발산'하기 때문에,
가우스 면의 전기장 크기
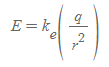
- 물리량
- r: 전하와 가우스면 사이의 거리
- q: 가우스면에 갇힌 전하
- [그림 3]과 같은 조건에서 구면상의 모든 점에서의 전기장과 법선벡터는 서로 평행하다.
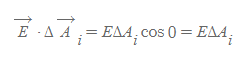
- 구면의 표면적은 4πr^2이므로, 닫힌곡면의 전기선속 식을 다음과 같이 계산 수 있다.
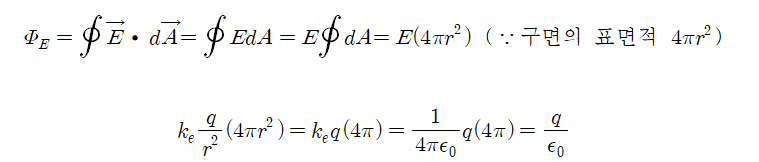
닫힌곡면의 전기선속
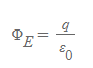
- 식에서 ε_0은 [33. 쿨롱의 법칙]에서 확인한 자유공간의 유전율이다.
- 의미: 구면을 통과하는 알짜 선속은 구면 내부에 존재하는 전하량에 비례한다.
가우스의 정리
가우스의 정리: 점전하 q를 둘러싼 닫힌곡면을 지나는 알짜 선속은 가우스 곡면의 모양과는 무관하고, 크기는 항상 q/ε_0으로 일정하다.

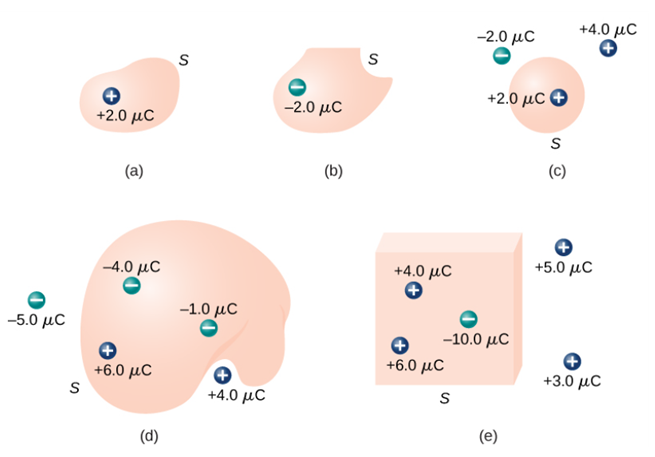
가우스의 정리와 법칙은 독일의 수학자이자 천문학자인 가우스(Carl Friedrich Gauss, 1777~1855)가 정리한 내용으로 아래의 내용이 큰 특징이다.
- 전하를 포함하지 않은 닫힌곡면에서의 알짜 전기 선속은 0이다.
- 가우스면 내부의 전하들이 여러 개라면 q=q_encl=q_1+q_2+...로 계산한다. e.g. 곡면 내에 같은 크기의 양전하와 음전하가 함께 있으면 알짜선속은 q+(-q)=0이다.[그림 4]
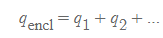
가우스의 법칙 Guass's Law
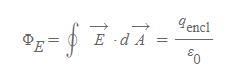
■
- 물리량
- 벡터 E: 미소 표면상의 각 전기장
- 벡터 A: 닫힌곡면인 가우스 곡면의 표면적 ⇒ 가우스 곡면은 전하에 대한 임의의 경계로 점선으로 표현한다.
- q_encl: 가우스 표면 내부의 알짜전하량
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 38. 대기와 지구 전기장 | Atmosphere and Electric Field (0) | 2023.09.23 |
|---|---|
| [물리학-전자기학] 37. 적용: 가우스의 법칙 | Applications: Gauss's Law (0) | 2023.09.23 |
| [물리학-전자기학] 34. 전기장 (1) | Electric Field (1) (0) | 2023.09.20 |
| [물리학-전자기학] 35. 전기장 (2) | Electric Field (2) (0) | 2023.09.20 |
| [물리학-전자기학] 33. 쿨롱의 법칙 | Coulomb's Law (0) | 2023.09.18 |