728x90
반응형

전하 분포에 따른 가우스 법칙
Applications to Charge Distributions
가우스 면의 설정에 따라 가우스의 법칙은 다양한 결과 식을 갖는다.
- 주어진 대칭성에 의해 전기장의 크기가 일정한 크기의 상수가 되는 경우
- 전기장의 방향과 면 법선의 방향이 평행하는 경우, 스칼라곱은 EA이다. ⇒ cos0=1
- 전기장의 방향과 면 법선의 방향이 수직하는 경우, 스칼라곱은 0이다. ⇒ cos90=0
- 전기장이 가우스면 상에서 0이 되는 경우
가우스 법칙으로 표현한 일정한 크기의 전기장

■
도체 구 전하분포
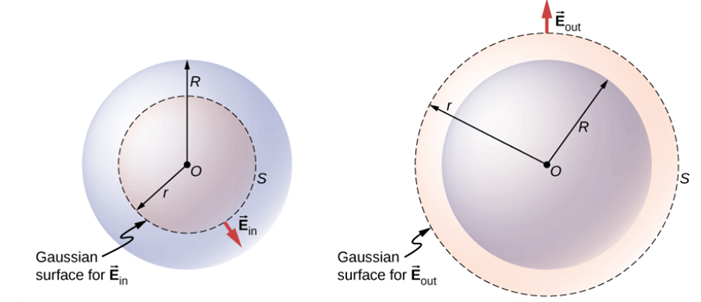
도체 구 전하분포의 전기장을 가우스 법칙으로 계산해보자.
구 외부, 한 점에서의 전기장 크기[그림 2]
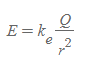
■
- 물리량
- Q: 가우스면에 속한 구체의 전하로 (부피전하밀도)x(부피)의 식을 만족한다.
- r: 도체 구의 중점으로부터 가우스 면까지의 거리[그림 1], r>R

구 내부, 한 점에서의 전기장 크기
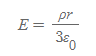
■
구 내부, 한 점에서의 전기장 크기
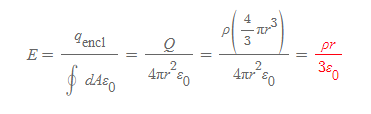
- 물리량
- Q: 가우스 면에 포함된 전하량 ⇒ Q=ρ(4πr^3/3) (r: 구체전하의 반지름)
- r: 구체의 중점에서부터 가우스 면까지의 거리 cf. R: 구체전하의 반지름
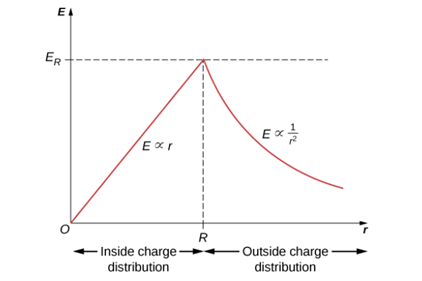
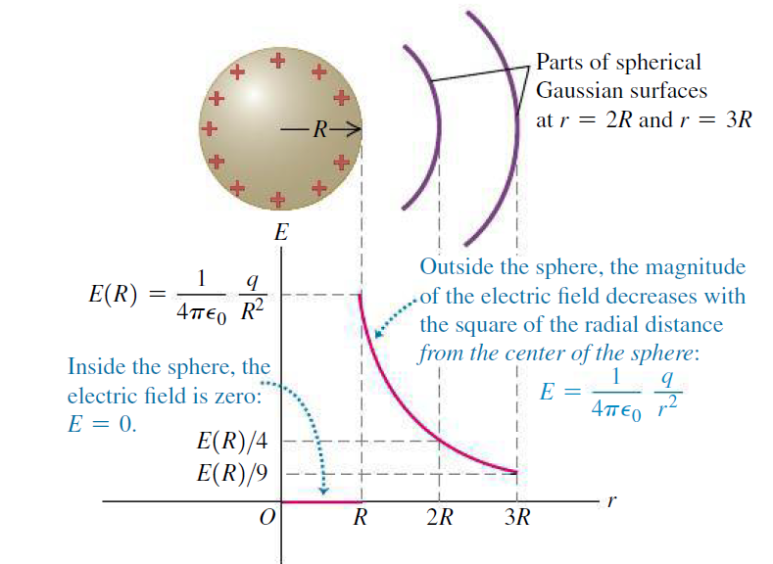
구 대칭 전하분포에 대한 가우스면을 어디에 설정하느냐에 따라, 전기장의 크기는 가우스 면 반지름 r에 비례하거나 혹은 제곱에 반비례할 수도 있다.[그림 3]
- 구 대칭 전하분포 내 가우스 면 반지름에 대해 전기장의 크기는 비례한다.
- 구 대칭 전하분포 외 가우스 면 반지름에 대해 전기장의 크기는 제곱에 반비례한다.
원통 대칭 전하분포
전하가 분포된 선이 무한히 길다고 설정하면, 점의 수직 위치에 상관없이 선으로부터 같은 거리에 있는 모든 점에서 전기장의 크기는 일정하다.
- 가우스 면은 원통 모양으로 선을 감싼 형태[그림 4]로 가우스 면에 같은 전하량은 다음과 같다.
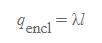
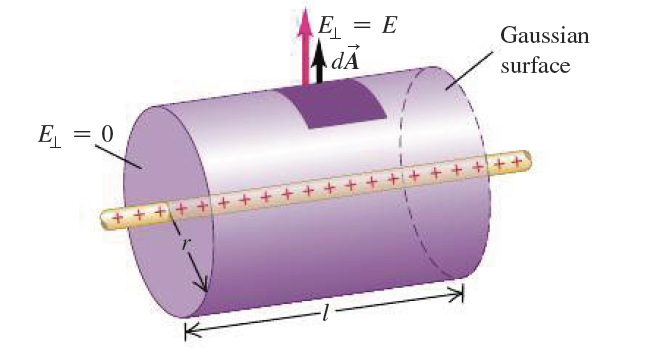
원통 대칭 전기장 크기

원통 대칭 전기장 크기
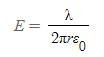
■
원통 대칭 전기장 크기에 쿨롱 상수를 적용하면 다음과 같이 식을 정리할 수도 있다.
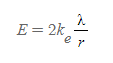
- 의미: 선전하분포의 경우, 전기장의 크기는 선전하 밀도에 비례하고, 떨어진 거리에 반비례한다.
평면 전하분포
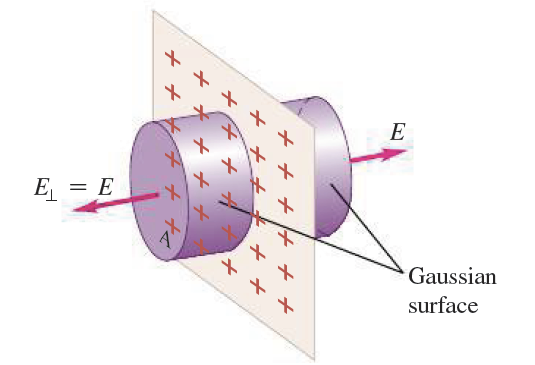
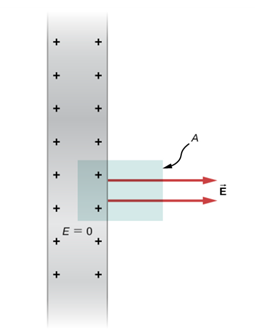
전하를 띤 평면이 무한히 크면[그림 5], 평면으로부터 떨어진 모든 점의 전기장 크기는 같다.
- 전기장은 모든 점에 대해 그 평면의 수직한 방향으로만 방사한다.
- 가우스 면의 설정: 평면에 수직인 축을 가지고 각각의 넓이가 A인 평면을 관통한 원통으로 곡면을 설정한다.
전하를 띈 평면을 관통한 가우스 곡면에 대한 전기 선속
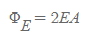
전체 가우스 면을 통과하는 전체 선속은 곡면 양 끝을 통과하는 선속의 총합과 같다. 만약, 가우스 곡면이 평면을 ‘뚫지 않은’ 원통[그림 6]이라면 전기 선속은 다음과 같다.
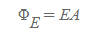
가우스 면에 포함된 전하는 σA(면전하분포)이다. ⇒ [36. 가우스의 법칙] 표면전하밀도 참고
평면전하의 전기장 크기
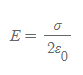
■
평면전하의 전기장 크기
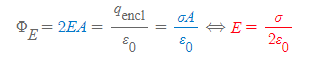
728x90
반응형
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 39. 전위 | Electric Potential(EP) (0) | 2023.09.25 |
|---|---|
| [물리학-전자기학] 38. 대기와 지구 전기장 | Atmosphere and Electric Field (0) | 2023.09.23 |
| [물리학-전자기학] 36. 가우스의 법칙 | Gauss's Law (0) | 2023.09.21 |
| [물리학-전자기학] 34. 전기장 (1) | Electric Field (1) (0) | 2023.09.20 |
| [물리학-전자기학] 35. 전기장 (2) | Electric Field (2) (0) | 2023.09.20 |