[물리학-전자기학] 39. 전위 | Electric Potential(EP)

 

전위 공식의 유도

Derivation of EP

 

전위(electric potential): EP, 전기장 내에서 단위전하가 갖는 위치에너지로, 스칼라량이다.

• 단위: [V](볼트, volt)
• 계산의 편의를 위해 지표면의 전위를 0V로 잡는다.
• 의미: 전기장 내의 기준점으로부터 어떤 지점까지 단위 전하를 옮기는 데 필요한 에너지의 양

​

전위의 의미를 쉽게 이해하기 위해 중력장에서 물체를 옮기는 경우를 떠올려보자.

 

그림 1. 일정한 중력장 내에서 질량의 이동 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.777]

 

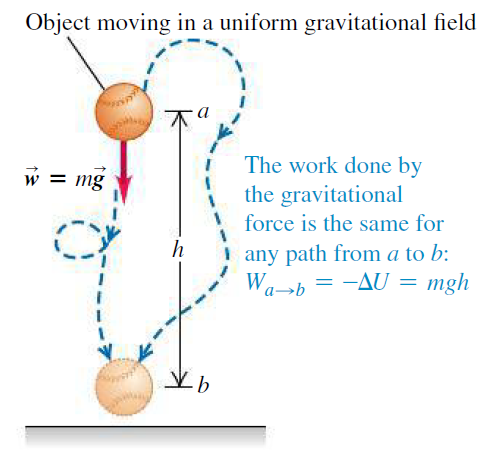
[그림 1]과 같이 물체를 a에서 b로 이동시킬 때, 중력은 보존력이므로 보존력이 한 일은 다음과 같이 쓴다.

• U_i: 초기 위치에서의 퍼텐셜 에너지
• U_f: 최종 위치에서의 퍼텐셜 에너지

​

쿨롱의 법칙으로 기술되는 전기력 역시 보존력으로 위의 식을 만족한다.

 

 

그리고 x축을 기준으로 보존력이 한 일은 다음과 같은 식을 만족함을 이미 배웠다.

그림 2. 일정한 전기장 내에서 전하의 이동 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.777]

 

우리는 [34. 전기장(1)]에서 전기장의 공식을 배웠기 때문에, 일 식에서 F를 다음과 같이 쓸 수 있다.

​

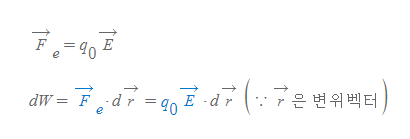
• 의미: 전기장 내의 점전하 q_0가 전기장에 의해 미소 변위 dy[그림 2]만큼 이동할 때, 전기장이 전하 q_0에 한 일은 위와 같이 쓸 수 있다.
• 일정한 전기장 내에서 미소 변위 움직임은 '미소 일'로 해석 가능하다.
• 전기력은 보존력이므로, W_conservative를 다음과 같이 쓸 수 있다.

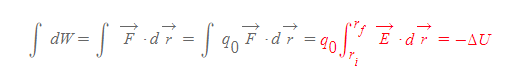
[그림 2]에서처럼 위의 W식을 (y축을 기준으로) a에서 b까지 이동시켰을 때의 내용으로 정리하면,

이다.

​

계의 위치에너지 변화를 기준으로 식은 아래와 같이 정리된다.

​

• f: 최종점
• i: 초기점

​

위 식에서 우리는 특정한 지점의 '전위'를 드디어 구할 수 있다.

​​​

U/q는 원천 전하의 분포에 의한 전위로 V라고 쓴다.

​

초기 위치에너지가 0일 때, 특정 지점에서의 전위

■

​

• 만약 시험전하가 처음 위치 a에서 나중 위치 b로 이동하고, ΔV가 (나중 전위)-(처음 전위)일 때, 식은 다음과 같이 정리된다.

​

두 점 사이의 전위차(전압)

​

■

• 물리량

1. U: 위치에너지
2. q_0: 단위전하
3. E: 일정한 크기의 전기장
4. d(벡터 s): 전기장 공간에서 두 점 사이의 변위

• 두 지점 사이의 전위차를 '전압(voltage)'이라 한다.
• 전기장 내의 특정 지점의 전위를 0이라 생각하고 문제를 풀면 쉬워 진다.
• 전위차는 원천 전하에 의해 발생한 것으로 원천 전하의 분포에 의존한다.
• 1쿨롱의 전하량을 1볼트(1 volt)만큼의 전위차만큼 옮기기 위해서는 1줄의 일이 필요하다.

​

1볼트의 정의

​

■