
원자의 퍼텐셜에너지
우리 주위의 물질은 원자라는 기본단위로 구성되어 있다. 하지만 사실 대부분의 물질은 독립된 원자가 아닌 '분자'가 최소 단위로 대부분 구성된다.
- 단, 비활성기체(18족 헬륨족 원소)는 상온 조건에서 안정한 단원자 상태로 본래는 원자이나 분자처럼 거동한다.
- 이원자분자(diatomic molecule): 상온 조건에서 두 개의 원자가 전자기력에 의해 결합한 형태(two atoms bonded together)로, 일반적인 수소, 질소, 산소 등을 일컫는다. [그림 1]

원자는 전하를 가진 소립자(전하 미립자로 양성자, 전자 등이 대표적)들의 집합체이고, 이들은 다른 원자의 소립자들과 서로 전자기적 상호작용을 한다. 소립자의 극성에 따라 인력 또는 반발력을 갖는다. [그림 2]
- 서로 같은 전하의 소립자가 마주치는 경우, 반발력(repulsive force)이 작용한다.
- 서로 다른 전하의 소립자가 마주치는 경우, 인력(attractive force)이 작용한다.

- 전자기적 상호작용을 통해 원자는 서로 뭉쳐서 분자가 된다. 그리고 뭉쳐진 이 분자 군(group)의 성격에 따라 물질의 상태(고체, 액체, 기체 상태 등)가 또한 결정된다.
원자 간의 퍼텐셜에너지 함수

[그림 3]은 원자 간의 위치에너지 함수로 입자간의 거리는 두 원자핵간 거리와 같다.
- x축은 두 원자 간의 거리, y축은 거리에 따른 퍼텐셜에너지의 변화를 뜻한다.
- 두 입자 사이가 무한히 떨어진 경우(r→∞), 두 입자 사이의 상호작용은 존재하지 않으므로, 에너지의 값을 0으로 기준잡는다.
- 두 원자가 각각 존재할 때, '안정할 경우'는 (-)의 퍼텐셜에너지 값을 갖고, '불안정할 경우'는 (+)의 퍼텐셜에너지 값을 갖는다. '안정한 경우'의 실제 세계에서의 모습은 서로 간의 소립자가 마주칠 때, 자연스러운 힘(인력 또는 반발력)이 나타나는 것이다.
- r: 기준 입자와 나머지 입자 사이의 거리
- r_m: 결합길이(bond length), 퍼텐셜에너지가 가장 낮은 지점에서의 두 원자 사이의 거리로, 두 원자가 가장 안정한(가장 낮은 퍼텐셜에너지 값을 가진) 분사 상태가 될 수 있는 지점과 같다.

(1)두 원자 간의 거리와 (2)내부의 소립자에 따라 인력과 반발력이 결정된다.
- [그림 4]는 수소 원자 간의 거리에 따른 에너지로 0.74A(옴스트롱) 거리가 bond length이며, 이때 에너지 값을 (최대)안정결합 에너지(stable bond energy)라 한다. 두 원자는 결합을 통해 가장 낮은 퍼텐셜에너지를 갖는다.
분자 간 결합
Intermolecular Forces
- 분자 간 결합: 원자의 결합을 통해 존재하는 분자 간 결합, 기체 상태의 분자들은 거의 독립적으로 운동하는 반면 액체나 고체는 분자와 분자 사이의 구성 부분 전하[그림 5]에 따라 다시 전기적으로 서로 붙을 수 있는데, 이와 관련된 모든 결합을 지칭한다.
- 분자는 점전하가 아닌 양전하, 음전하가 모두 들어간 복잡한 구조이므로 분자의 구조적 특성에 따라 쿨롱의 법칙을 별도로 설정해야 한다. ⇒ 분자의 구조 상 부분 전하가 적용된 지역에 대해 쿨롱의 법칙을 적용할 수 있다.

중성의 두 분자가 가까워지는 경우, 한 분자 내의 핵과 전자가 다른 분자의 핵과 전자와 동시에 상호작용하여, 두 분자 사이에 새로운 퍼텐셜에너지가 발생한다.
- 두 분자가 아주 먼 거리로 떨어진 경우, 분자 간의 상호작용이 거의 일어나지 않기 때문에 계(system)의 퍼텐셜에너지를 0으로 둘 수 있다. 여기서 계란, 두 분자를 모두 포함한 상호작용을 뜻한다.
- 분자가 서로 가까워지기 시작하면 정전기적 인력이 정전기적 반발력보다 커진다. ⇒ 정전기적 인력 퍼텐셜 에너지(attractive potential energy)의 값이 커진다.
- 분자간의 거리가 극도로 짧아지면 반발력이 인력보다 커진다. ⇒ 정전기적 반발력 퍼텐셜 에너지(repulsive potential energy)의 값이 커진다.
여기서 인력, 반발력 퍼텐셜에너지 값은 다음과 같이 구한다.
힘, 일, 퍼텐셜에너지 구하기

- F_a: 인력 / F_r: 반발력 / q_m(molecule): 분자의 구조(structure)에 걸린 총 전하량 / r: 두 분자 사이의 거리
- k는 쿨롱의 법칙에 나타난 쿨롱 상수로 1/4πε_0로 계산된다.
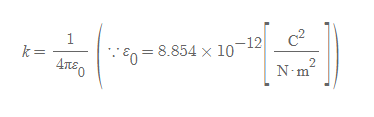
- 분자들 사이에 인력이 작용하면 F는 음수 부호를 갖는다. F는 분자 사이에 작용하는 정전기력을 의미하고, 분자의 기하학적 구조에 따라 특정 전하량을 가진 것으로 취급할 수 있다.
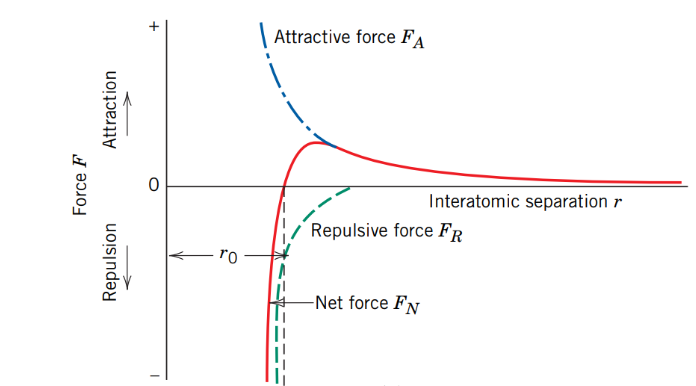
[그림 6]에 따르면, 분자 간 결합은 그 길이에 따라 인력, 반발력의 지배력 차이를 갖는다. 즉, bond length를 기준으로 (1)결합길이 이전(결합길이보다 긴 결합 거리)까지는 인력이 지배적이고, (2)결합길이에서는 두 힘의 크기가 (벡터합이) 0이 되며, 마지막으로 (3)결합길이보다 짧은 길이에서는 반발력이 지배적이다. ⇒ [그림 6]의 net force가 attraction 영역에 있는지, 아니면 repulsion 영역에 있는 지에 따라 지배하는 힘을 판단할 수 있다.
- 일(work) 공식에 따르면, 힘의 방향과 물체의 이동방향이 같으면 크기가 더 증가하는 값을 갖게 되는데, 이때 퍼텐셜에너지와의 일반적인 관계식은 다음과 같다.

- 전기적 힘은 인력, 반발력의 2가지 형태로 나뉘고, 그 값을 일 공식에 대입하면 (1)인력이 한 일은 음수, (2)반발력이 한 일은 양수로 계산된다. 적분의 상한, 하한은 무한대의 거리(r_∞)로 떨어진 상태에서 bond length(r)까지 두 분자 사이를 좁히는 것으로 가정한다.
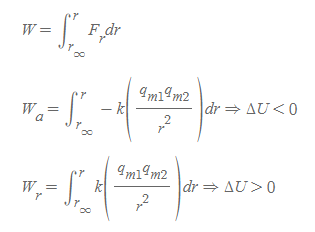
- W_a는 인력에 의해 한 일로, 두 분자 사이의 거리를 좁힐 수록 더 큰 음수 값을 갖게 된다.
- W_r은 반발력에 의해 한 일로, 두 분자 사이의 거리를 좁힐 수록 더 큰 양수 값을 갖게 된다.
- W=U_f-U_i의 공식에 따라 위의 두 내용은 [그림 7]과 같은 그래프로 나타나는 데, [그림 7]의 total energy curve는 각 퍼텐셜에너지의 값을 모두 합한 알짜(net) 값에 해당한다.
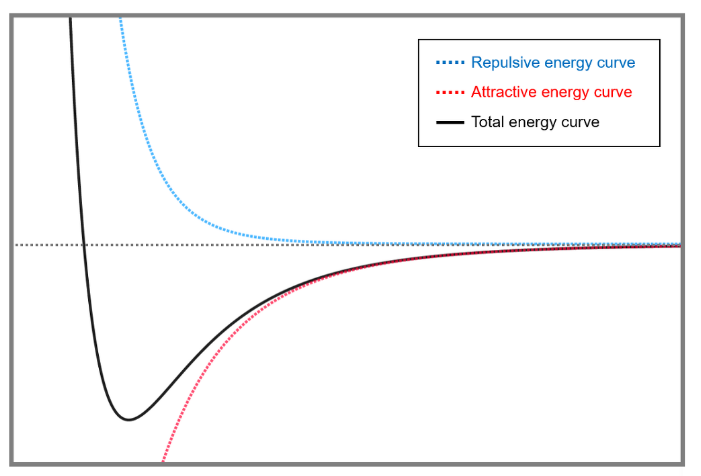
분자 간 인력 퍼텐셜에너지

■
분자 간 반발력 퍼텐셜에너지

■
'대학화학' 카테고리의 다른 글
| [대학화학 - 통계열화학] 분자간의 상호작용 - 퍼텐셜에너지의 이해 (2) (0) | 2023.09.11 |
|---|---|
| [G. Chem] 열화학 기초 | Basic Ideas of Thermodynamics (0) | 2020.04.19 |
| [G. Chem] 20. 마델룽 상수(Madelung Constant) (0) | 2020.04.11 |
| [G. Chem] 19. 격자에너지(Lattice Energy) (0) | 2020.04.11 |
| [G. Chem] 18. 전기음성도(Eletronegativity) (0) | 2020.04.11 |