
앞선 챕터(분자간의 상호작용 - 퍼텐셜에너지의 이해 (1))의 분자 간 결합에서 우리는 퍼텐셜에너지의 빠른 이해를 위해 분자의 실질적인 운동에너지를 고려하지 않았다. 하지만, 앞으로 분자간의 상호작용에서 사용하게 될 실질적인 퍼텐셜에너지 공식은 (1)전자기력은 경로에 의존하지 않는(경로비의존성) 보존력이며, (2)따라서 이 보존력은 '역학적 에너지 보존법칙'을 만족한다는 사실로부터 새롭게 유도하도록 한다.
보존력
보존력의 특징 중 대표적인 것은 어떤 물체가 보존력에 의해 지점 A에서 운동을 시작하여 지점 B에 운동을 완료했다면, 어떤 경로를 거쳤던 간에 보존력이 한 일은 항상 같다는 사실이다. [그림 1]

- 보존력이 한 일은 가역적이다.
- 보존력이 한 일은 경로에 무관하다. 즉, 출발점과 도착점에만 그 값이 의존한다.
- 만약 출발점과 도착점이 동일하다면 전체 보존력의 한 일은 0이다. 닫힌 경로(closed path)에서 보존력이 한 일은 0이다.
- 보존력의 일은 퍼텐셜에너지 함수의 처음 값과 나중 값의 차이로 표현된다.
보존력의 여러가지 특징 중 4번의 내용을 구하기 위해 '역학적 에너지 보존의 법칙'을 알아보자.
역학적 에너지 보존의 법칙
어떤 물체의 역학적 에너지는 마찰력이나 공기저항과 같은 비보존력이 없는 한, 내부에너지의 변화가 없고 따라서 '역학적 에너지'는 항상 보존된다. 여기서 역학적 에너지는 물체의 운동에너지와 퍼텐셜에너지의 총합을 의미한다.
일과 운동에너지의 관계식

역학적 에너지의 총합

- 어떤 물체의 역학적 에너지는 그 물체의 운동에너지에 퍼텐셜에너지를 더한 값이고, 이는 경로와 상관없이 항상 일정한 값[그림 2]을 갖는다.


일과 운동에너지의 관계식과 역학적 에너지의 합을 잘 조합하면, '보존력이 한 일'과 '보존력에 의한 퍼텐셜에너지'의 관계식을 세울 수 있다.
[1] 역학적 에너지의 합 공식 재조합

[2] 보존력이 한 일 = -Δ(보존력에 의한 퍼텐셜에너지) = 처음 퍼텐셜에너지 - 나중 퍼텐셜에너지

- 상호작용하는 두 분자를 무한소 거리만큼 이동시킬 때, 거리는 dr로 표현할 수 있고, 이때 한 일은 아래와 같이 표현된다. ⇒ 분자의 이동은 그 자체로 매우 작은 거리이기 때문에 실측 계산 기준으로 이는 무한소로 간주해도 무난하다.

보존력

■
- 보존력 식에서 나타나는 음수부호는 항상 계가 가장 낮은 위치에너지를 갖도록 작용하는 보존력의 특성을 나타낸다.
- 퍼텐셜에너지는 물체의 위치에 따라 정해지는 함수이므로 U(r)로 표현된다. 마찬가지로 보존력 또한 물체의 위치에 의해서 그 힘의 크기가 달라지기 때문에, F(r)로 표현한다.
- 화학에서 원자, 분자의 퍼텐셜에너지는 U 대신 V로도 자주 쓴다. 따라서 앞으로는 U보다 V를 더욱 활용하도록 한다.
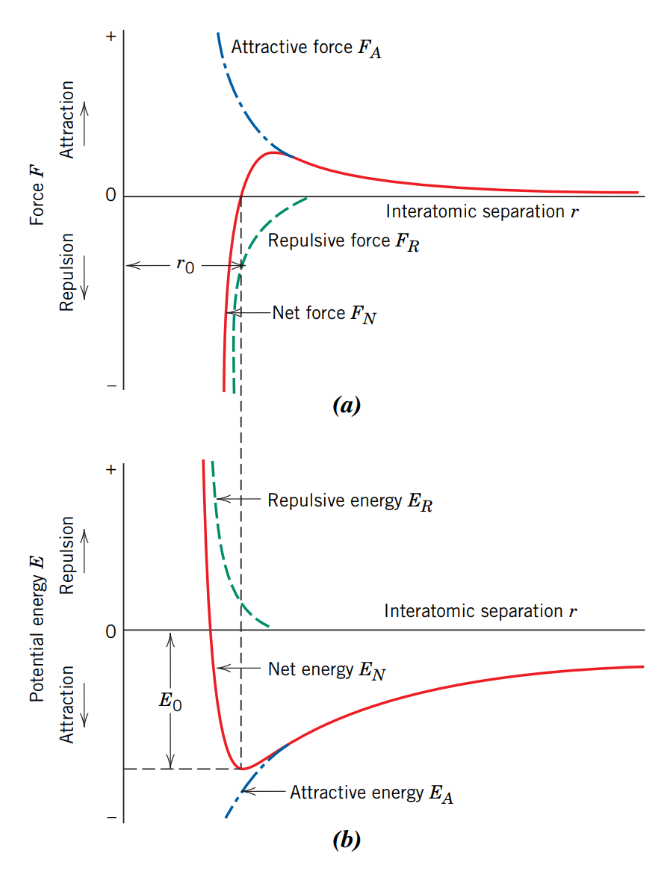
보존력 식을 통해 먼저 나중 퍼텐셜에너지 값을 구할 수 있는 식을 유도해보자.

분자 간 인력 퍼텐셜에너지 또는 반발력 퍼텐셜에너지를 보존력 식에 대입하면, (보존력의 특성을 지닌) 전기적 인력 또는 반발력 식을 얻을 수 있다.
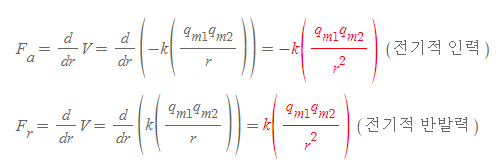
'대학화학' 카테고리의 다른 글
| [대학화학 - 통계열화학] 분자간의 상호작용 - 퍼텐셜에너지의 이해 (1) (0) | 2023.09.10 |
|---|---|
| [G. Chem] 열화학 기초 | Basic Ideas of Thermodynamics (0) | 2020.04.19 |
| [G. Chem] 20. 마델룽 상수(Madelung Constant) (0) | 2020.04.11 |
| [G. Chem] 19. 격자에너지(Lattice Energy) (0) | 2020.04.11 |
| [G. Chem] 18. 전기음성도(Eletronegativity) (0) | 2020.04.11 |