
RC 회로(RC circuits): 축전기(C), 전지, 그리고 저항(R)을 직렬로 연결했을 때 직류회로
- 저항기와 축전기로 구성되어 있음
- 두 소자는 직렬로 연결되어 있음
- 전지에 의해 축전기는 충전과 방전의 단계를 거친다.
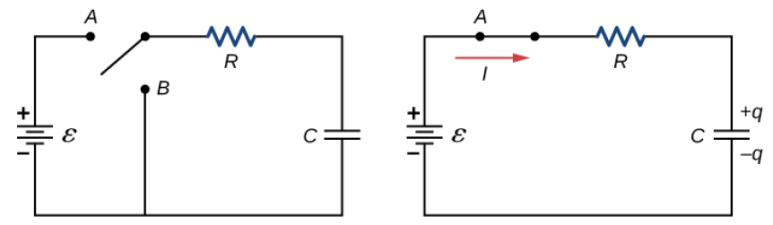
[그림 1]에서 왼쪽 그림은 스위치에 의해 회로가 연결되기 전의 RC 회로를 뜻한다. 이때 스위치를 A지점에 연결시키면, 전류는 [그림 1]의 오른쪽 그림과 같이 흐르는데, 이때 축전기는 '충전'된다.
RC 회로의 충전
Charging a Capacitor
RC회로에서 축전기의 충전 단계를 분석하면 다음과 같다. ⇒ 키르히호프의 법칙을 적용
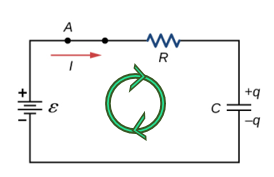
- [그림 2]는 분기점이 없는 RC회로로 전류의 방향을 위와 같이 임의로 설정할 수 있다.
- 다음 폐회로에 travel을 시계방향과 같이 그린다.
키르히호프 규칙에서 전류 I의 방향과 순환 고리 travel의 두 방향성에 따라 전압 강하의 부호가 결정되었다.
- 전류의 방향과 travel의 방향이 서로 같을 때, 저항에서 전압을 소모(-)한다.
- 전류의 방향과 travel의 방향이 서로 같을 때, 축전기는 전지의 에너지를 소모(-)함으로써 자신의 에너지를 충전한다.
고리법칙은 앞선 챕터에서 계속 배웠듯, ∑ε(기전력)+∑ΔV(전압강하 소자) = 0인 식을 따르고, 전압강하를 일으키는 소자 (1)저항 ΔV=IR, (2)축전기 ΔV=q/C 식을 적용해 다양한 물리량을 구할 수 있다.
축전기의 ΔV는 전기용량(정전용량) C를 [전자기학_13. 전기용량(커패시턴스)]에서 배우면서, 이미 유도해보았다.
[물리학-전자기학] 13. 정전용량(커패시턴스) | Capacitance (1)
정전용량(capacitance): 전기용량, 커패시턴스, 유전물질(유전체)이 전하를 축적할 수 있는 능력 cf. 축전...
blog.naver.com
RC 회로에서 충전과정은 다음 고리 법칙 식을 만족한다.

- 물리량
- q/C: 축전기에서의 전위차 ⇒ (축전기의) 양판에서 음판으로 전류방향과 travel 방향이 평행하기 때문에 축전기에 전하량은 충전된다.
- IR: 저항에서의 전압 강하 ⇒ 저항을 흐르는 전류 방향과 travel 방향이 평행하기 때문에 저항은 전기적 퍼텐셜에너지를 소비한다.
이때, q와 I는 각각 충전기가 충전될 때 시간에 의존하는 순간 전하와 순간 전류를 의미한다. ⇒ 일정한 전류 값을 가지는 정상상태가 아님에 유의한다.
t=0 조건
[1] 스위치를 닫는 순간으로 축전기의 전하(전하량)는 0이며, 고리 법칙 식으로부터 처음 전류를 구할 수 있다.
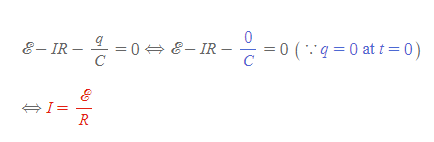
이때 I를 t=0 조건에서 RC회로의 최대 전류라 정의한다.
RC회로의 최대전류
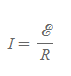
■
전지 단자로부터의 전위차는 저항기에 기인한다.
축전기 완충 상태
축전기가 최대 전하량 Q로 충전되면 전하의 흐름은 멈추고 회로의 전류는 0이 된다.
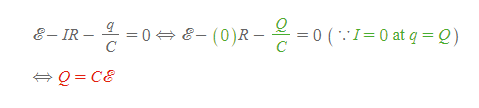
RC회로의 최대충전량
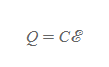
■
다음은 시간에 따라 변하는 전하와 전류를 아래와 같이 구해보자.
RC회로 충전전기량
[1] RC 회로의 고리 법칙 식에 ×(1/R)을 하고 I는 미분형으로 표현한다.
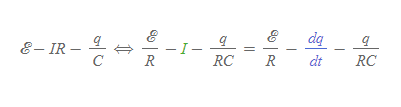
[2] dq/dt를 우변으로 넘긴 뒤, 아래와 같이 통분하여 새로운 식을 쓴다.
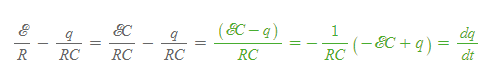
[3] [과정 2]의 식을 적분하기 위해 아래와 같이 식을 변경한다.
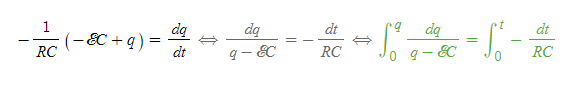
[4] [과정 3]의 초록색 식의 왼쪽 식은 치환적분으로 풀 수 있다.
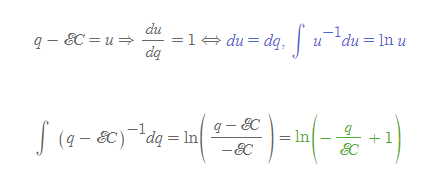
[5] [과정 3]의 초록색 식의 오른쪽 식은 -(t/RC)이다.
[6] [과정 4]와 [과정 5]의 두 식은 서로 같으므로 아래와 같이 정리할 수 있다.
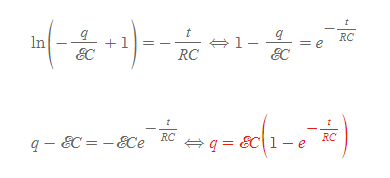
- [과정 6]의 두 번째 과정은 양변에 εC를 곱하여 유도했다.
q.e.d.
RC회로 충전전기량
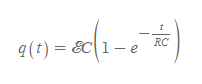
■
- 의미: RC회로에서 충전 중인 축전기에서 시간에 따라 충전되는 전하량 함수
- t의 시간이 무한대로 가면 Q=εC(기전력×전기용량)을 만족한다.
RC회로 충전전기량 식을 시간에 대해 미분하면 RC회로에서 시간에 따른 전류의 함수를 구할 수 있다.
RC회로 전류(시간)함수

■
- RC회로 전류 함수에서 ε/R은 RC회로의 최대전류 값이다.
축전기에 전하가 충전되면 전하량 q는 시간에 따라 지수적으로 증가하다가 충전이 끝나면 최대충전량을 갖는다. 마찬가지로 전류 I는 시간에 따라 지수적으로 감소하다가 축전기의 충전이 끝나면 0[A]가 된다.
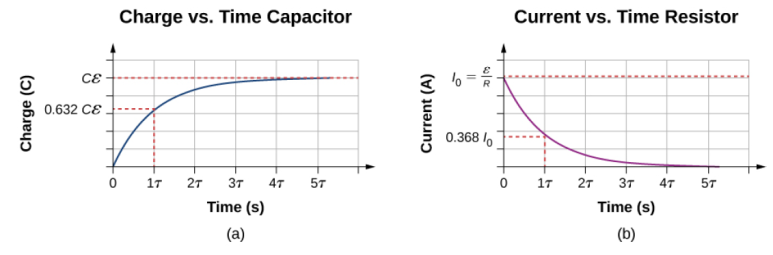
RC회로의 물리법칙은 그래프로 표현했을 때 지수함수[그림 3]적인 특징을 가지는데, 지수함수 그래프를 그리는 많은 물리량은 충분한 시간을 조건으로 점근선의 최댓값에 '근접'할 수는 있지만, 그 시간이 무한대로 필요하다는 현실적 한계가 있다. 따라서 성능의 근사적 도달시간으로 특히 전자기학에서는 시상수 τ(타우, tau)라는 새로운 개념을 도입했다.
- 지수함수적 증가 그래프에서 시상수에 도달하면 최댓값의 약 63.2%에 달한다.
- 지수함수적 감소 그래프에서 시상수에 도달하면 최댓값의 약 36.8%로 감소한다.
RC회로 시간상수
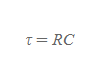
■
의미: RC회로의 시간 상수로 전류가 처음 값의 1/e로 감소하는 데 걸리는 시간
- [그림 3]에서 1τ의 시간이 지났을 때, (1)전하량은 최대치를 기준으로 약 63%에 도달하였고, (2)전류 크기는 최대치를 기준으로 약 36%로 감소하였다.
RC 회로의 방전
Discharging a Capacitor
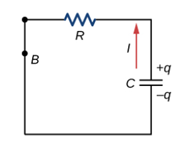
[그림 4]와 같이 전지의 연결이 사라졌을 때, RC회로에서 축전기는 방전 단계로 돌입한다.
- 회로에 전지가 없는 것을 제외하고 충전상황과 동일하다. 그러므로 충전상황의 식에서 기전력만 제거한다.
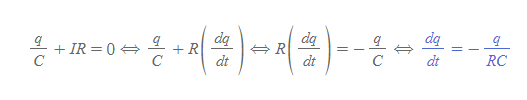
RC회로 방전전기량
[1] 위의 식을 적분한다.
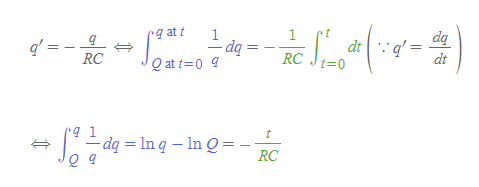
[2] ln을 소거하기 위해 지수함수를 취한다.
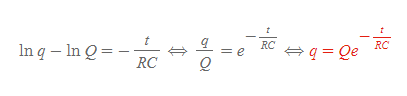
RC회로 방전전기량
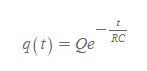
■
RC회로 방전전류(시간)함수
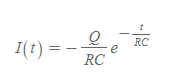
■
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 28. 자석과 자성 | Magnets and Magnetism (0) | 2023.11.30 |
|---|---|
| [물리학-전자기학] 27. RC회로의 특징과 시간상수(시상수) | Features of RC Circuits and Time Constant (0) | 2023.11.20 |
| [물리학-전자기학] 24. 키르히호프 규칙 | Kirchhoff's Rule (0) | 2023.11.19 |
| [물리학-전자기학] 25. 적용: 키르히호프 규칙 | Application: Kirchhoff's Rule (0) | 2023.11.18 |
| [물리학-전자기학] 23. 드루드의 전기전도모형 | Drude's Electrical Conduction Model (0) | 2023.10.26 |