[물리학-전자기학] 27. RC회로의 특징과 시간상수(시상수) | Features of RC Circuits and Time Constant

 

이번 챕터에서는 [전자기학_26. RC회로]에서 배운 RC회로의 특징을 다시 정리하고, 시상수에 대해서 좀 더 알아보도록 한다.

https://blog.naver.com/sortie0228/223268922292

[물리학-전자기학] 26. RC 회로 | RC Circuits

 

RC 회로의 특징

Features of RC Circuits

 

직류가 흐르는 RC 회로는 크게 (1)충전과 (2)방전의 단계로 구분하고, 이는 회로도로 표현하면 각각 다음과 같다.

​

충전단계[그림 1]

 

그림 1. RC회로 충전 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.886]

 

 

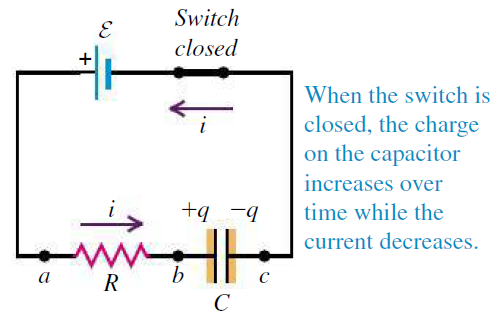
• 회로는 전지, 저항, 그리고 축전기(콘덴서)로 구성되어 있다.
• 전지의 기전력에 의해 저항과 축전기에 전류가 흐른다. 저항은 전기에너지를 사용해 일을 한다. 축전기는 전기에너지를 충전한다.
• 충전이 시작되는 시점에 전류는 최댓값을 갖는다. 반면 축전기의 충전 전하량 q는 0이다.
• 충전이 완료되는 시점에 전류는 0이 된다. 반면 축전기의 충전 전하량은 q이다.
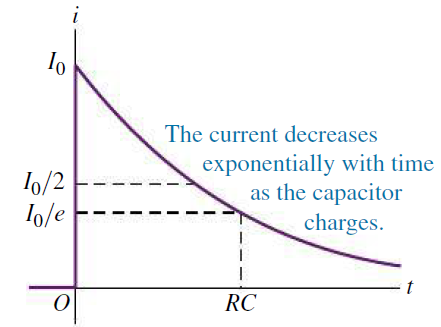
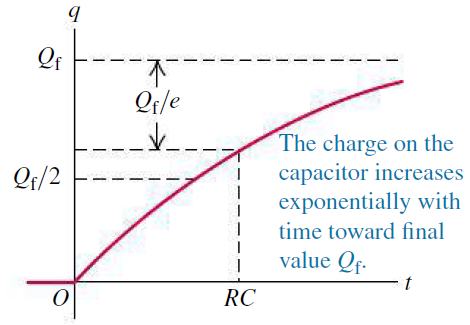
• 충전이 진행될 때, 충전 중인 전기량[그림 3]과 충전 전류함수[그림 2]는 시간에 의존한 함수의 꼴이다.

​

그림 2. RC회로 충전 시, 충전 전류함수 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.887]

 

​

 

 

그림 3. RC회로 충전 시, 충전전기량 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.887]

 

 

방전단계[그림 4]

 

그림 4. RC회로의 방전 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.889]

 

 

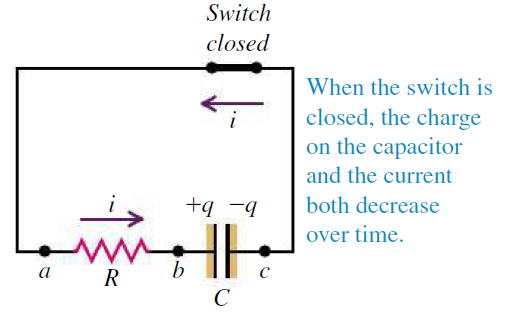
• 회로는 전지가 제외된 저항, 축전기(콘덴서)로 구성되어 있다.
• [그림 4]와 같이 스위치가 닫혔을 때, 축전기의 전하량과 전류는 시간이 지남에 따라 점차 감소한다.
• 스위치가 닫히는 시점에 전류는 최댓값을 갖는다. 단 부호는 (-)이다.
• 스위치가 닫히는 시점에 축전기에 쌓인 전하 Q_0는 최댓값이다.
• 스위치가 닫히고 시간이 지날 수록 회로에 흐르는 전류와 축전기에 쌓인 전하량은 점차 감소한다. 마찬가지로 방전전기량[그림 6]과 방전전류함수[그림 5]는 시간에 의존한 함수의 꼴이다.

​

 

그림 5. RC회로의 방전 시, 방전 전류함수 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.889]

 

​

그림 6. RC회로의 방전 시, 방전전하량 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.889]

 

RC회로의 두 가지 단계에 나타나는 다양한 물리량을 아래와 같은 도표로 정리할 수 있다.

 

 

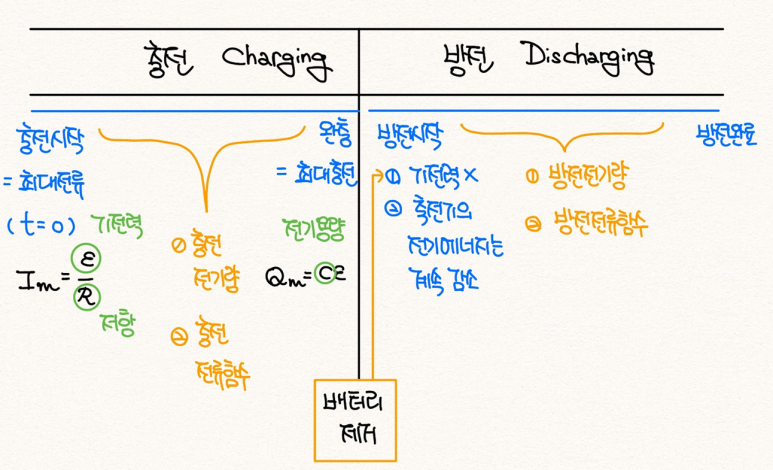
• 키르히호프 규칙을 사용하여, 충전시작점과 완충지점에서 각각 RC회로의 최대전류와 RC회로의 최대충전량을 계산할 수 있다.
• 충전과 방전이 발생하는 시간 t동안 시간에 의존한 함수는 총 4가지이다.

1. 충전전기량
2. 충전전류함수
3. 방전전기량
4. 방전전류함수

 

 

​

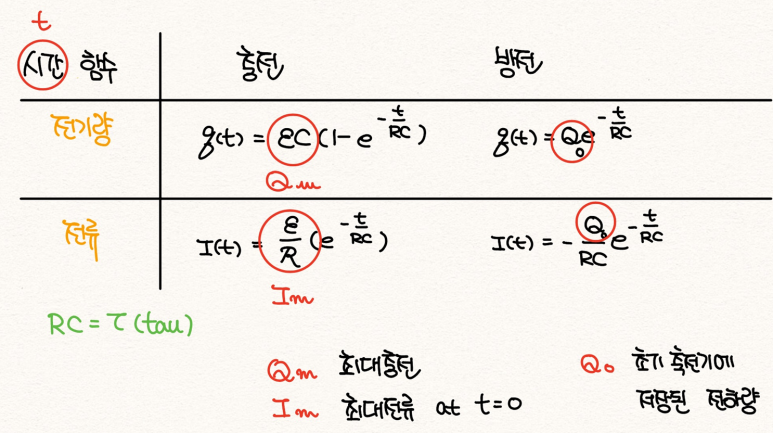
4가지 공식에서 나타나는 다양한 물리량을 활용하면, 더욱 식을 쉽게 쓸 수 있다.

• 시상수: RC = τ
• Q_m: RC회로의 최대 충전량
• I_m: RC회로의 최대 전류
• Q_0: 방전 시 최초 축전기에 저장된 전하량

​

시간상수(시상수)

Time Constant

 

RC회로의 물리량은 과도응답(transient response)의 그래프 특성을 갖는다.

• 시스템의 과도응답이란, 정상 상태(steady state)가 되기 전까지 걸리는 시간에 따라 나타나는 응답의 형태로 [그림 7]과 같은 그래프 형태로 나타난다.

 

그림 7

 

 

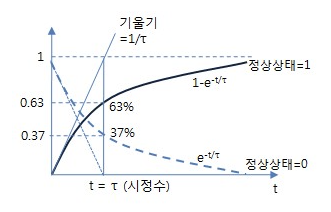
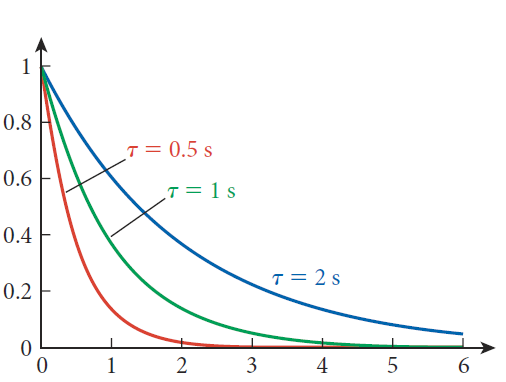
• 시스템이 주어진 변화에 대해 얼마나 빨리 응답할 수 있는 가를 나타내는 지표로, 시상수(시간상수, 시정수)는 특별히 (1)최종 정상상태의 약 63%까지 증가하는 데 걸리는 시간 또는 (2)초기 정상상태의 약 37%까지 감소하는 데 걸리는 시간을 의미한다.

​

과도응답의 후(後) 지속시간은 시상수 τ에 의해 결정된다.

​

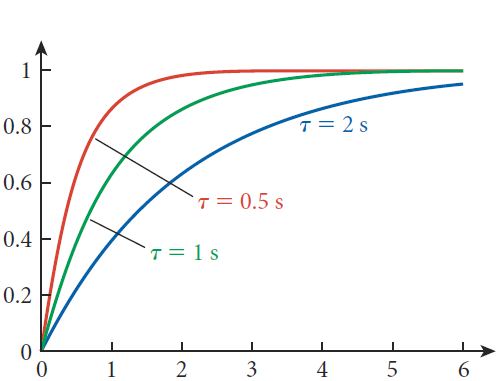
예를 들어, 충전 시 시상수가 짧을 수록 [그림 8]과 같이 전하량이 빨리 충전(q=1)되고, 전류는 [그림 9]와 같이 더 빨리 멈출 것(I=0)이다. 아래 두 그림의 x축은 모두 시간 축이다.

 

그림 8

 

 

그림 9