
우리는 [고전역학 - 20. 일과 에너지 1]에서 에너지를 다음과 같이 정의 및 분류했다.
- 에너지는 계의 경계를 넘어가며 전달되는데, 이들 유형 중 하나가 일(work)이다.
- 일(work): 외력과 작용점의 변위에 의해 에너지가 전달되는 방법
- 일은 힘과 힘이 작용하는 방향으로의 이동거리의 곱으로 크기가 정의된다.
증분 일(increment of work)은 dW로 적으며, 힘과 미소변위(infinitesimal displacement)의 스칼라곱으로 정의된다.
증분 일 | Increment of Work

■
- 물리량
- 벡터 F: 힘
- d(벡터 r): 미소변위
증분 일은 미소변위에 의해 결정된 미소 일 크기 값으로 만약 어떤 경로[그림 1]를 따라 변위 r이 정해진다면, 전체 일은 다음과 같이 정의된다.
일 | Work

■

일의 공식을 풀어쓰면 두 벡터 사이의 cosine 각도[그림 2]가 나오는데, 이 때문에 두 벡터 간의 각도가 평행하면 cos0=+1 또는 -1이되어 W=+W 또는 -W로 계산되고, 두 벡터가 서로 수직(perpendicular)하면 cos90=0이 되어 W=0이 된다.

운동에너지
Kinetic Energy
운동에너지를 유도하는 간단한 방법은 토리첼리 식(Torricelli's equation)으로부터 유도하는 것이다.

왼쪽의 토리첼리 식에 등가속도 운동을 하는 물체의 질량 m과 1/2을 양변에 곱해준다. 그러면,

이 나오는데, 여기서 maΔx는 FΔx = W (x-축에서의) 일의 값과 같고, 나머지 mv^2/2은 운동에너지로 정의한다.

일-운동에너지 정리 | Work-Energy Theorem

■
만약 경로 A에서 B로 이동한 경우, 일-운동에너지 정리는 아래와 같이 변형하여 쓸 수 있다.

- W_net이란, 알짜 일로 물체에 주어진 모든 힘의 알짜 힘에 의한 일을 의미한다.

위의 유도 방식은 뉴턴의 운동 제2법칙과 일 식을 조합이다.
운동에너지 | Kinetic Energy
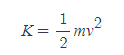
■
- 운동에너지는 입자의 운동으로 나타난 수치화된 에너지로 스칼라량이다.
- 운동에너지는 음의 값을 가지지 않는다.
- 단위: [J](Joule)
- 일-운동에너지 정리 부호
- 알짜힘의 방향이 운동방향과 같으면 한 일이 (+)이므로, 운동에너지는 증가한다.
- 알짜힘의 방향이 운동방향과 반대이면 한 일이 (-)이므로, 운동에너지는 감소한다.
퍼텐셜에너지
Potential Energy
물리학에서 퍼텐셜에너지란, 물체가 힘을 받고 있을 때 특정한 위치에서 가용한 에너지를 의미한다.
- 물체가 어떠한 위치에 존재함으로써 '잠정적'으로 얼마만큼의 일을 할 수 있는 지 알려준다.
- 핵심적인 퍼텐셜에너지는 총 6가지 종류로 다음과 같다.
- 중력 퍼텐셜에너지
- 탄성력 퍼텐셜에너지
- 만유인력 퍼텐셜에너지
- 전기 퍼텐셜에너지
- 전기 쌍극자 퍼텐셜에너지
- 자기 쌍극자 퍼텐셜에너지
퍼텐셜에너지는 한 위치에서 다른 위치로 물체가 이동할 때 '일이 경로에 무관한 힘'에 대해서만 정의되는 특징을 갖는다. 그리고 이러한 힘을 보존력(conservative force)이라고 하는데, (1)보존력만 작용하면 역학적 에너지가 보존되고, (2)수학적으로 보존력의 변위에 대한 적분은 경로독립적인 특징을 지닌다.
퍼텐셜에너지는 U 또는 V, E_p 등으로 다양하게 표현되며, 퍼텐셜에너지의 차이는 work의 개념을 도입해 다음과 같이 정의된다.
퍼텐셜에너지 차이 | Potential Energy Difference (PE Difference)
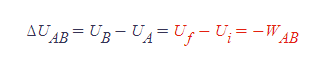
■
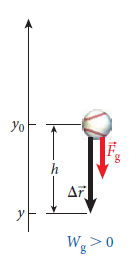
만약 [그림 3]과 같이 중력에 의해 야구공이 떨어진다고 할 때, 중력의 방향과 변위의 방향은 서로 평행하므로, 중력에 의한 일 W>0일 것이다.

그러나 퍼텐셜에너지는 떨어지면서 점차 감소하므로, 퍼텐셜에너지 차이의 부호 또한 음수가 될 것이다.
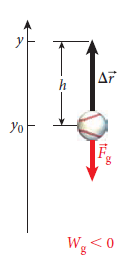
반면 [그림 4]와 같이 중력과 반대방향으로 야구공이 지면으로부터 멀어질 때, 중력에 의한 일은 W<0이고,

퍼텐셜에너지 차이의 부호는 양수가 될 것이다.
퍼텐셜에너지 차이에 적분형 일 공식을 적용할 수도 있다.
퍼텐셜에너지 차이 | PE Difference
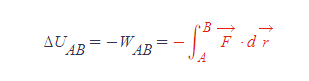
■
다음 장에서는 보존력의 판별과 다양한 퍼텐셜에너지 차이 식을 보도록 한다.
'고급물리학 > 고전역학' 카테고리의 다른 글
| [물리학-고전역학] 49. 벡터 미적분학: 컬(회전) | Curl (0) | 2024.01.02 |
|---|---|
| [물리학-고전역학] 48. 벡터 미적분학: 다이버전스(발산) | Divergence (0) | 2024.01.01 |
| [물리학-고전역학] 47. 벡터 미적분학: 그래디언트(기울기) | Gradient (0) | 2023.12.30 |
| [물리학-고전역학] 46. 토크 2 | Torque (2) (2) | 2023.12.24 |
| [물리학-고전역학] 45. 물리학 고전읽기: 칸트의 물리적 모나드론(1756) | Monadologia Physica (0) | 2023.12.14 |