Herald-Lab
【물리학 - 양자역학】 02. 흑체복사 본문

흑체와 흑체복사
Blackbody and Its Radiation
흑체(blackbody): 모든 파장의 전자기파를 완전히 흡수하는 가상의 물체로, 흡수율은 1로 하고 반사하지 않는다.
- 입사된 모든 복사를 흡수하는 이상적인 시스템으로 [그림 1]과 같이 내부가 비어 있고 작은 구멍이 나 있는 검은 물체를 가정한다.
- 빛을 완전히 흡수하므로 검게 보일 것이라 가정하였고(키르히호프, 1860), 온도에 의해서만 열복사(thermal radiation)를 한다. ⇒ 흑체가 흡수한 에너지의 방출은 전자기파 형태의 열복사를 띠며, 이때는 온도에만 의존한다. 즉, 온도에 따라 파장별 복사 세기의 분포가 달라진다.

- 흑체의 에너지 흡수: (흑체의) 속이 빈 공간 외부로부터 복사 에너지가 들어갈 때, 복사 에너지는 안쪽 벽에서 여러 차례 반사를 반복하나 빠져나가지 못한다. ⇒ 흑체의 구멍은 흡수체 역할을 한다.
열복사 | Thermal Radiation
임의의 온도에서 물체는 열복사 에너지를 방출하는데, 이 복사는 물체의 온도와 표면 특성에 의존한다.
- 열복사는 파장의 형태를 띠며, 표면의 온도가 증가할수록 적외선 영역에서 가시광선 빛 영역까지 열복사가 나타난다.
- 특히 백색광의 경우, 전자기 스펙트럼의 모든 부분에 해당하는 파장의 연속분포로 이루어져 있다.

뜨거운 석탄[그림 2]에서 뿜는 빛은 열복사의 예로 이 빛의 색깔은 석탄 조각의 온도에만 의존한다.
고전 전자기학에서 열복사는 물체 표면 근처의 가속 대전입자에 의해서만 발생한다. 즉, 열적으로 들뜬 전하는 가속도를 가지며 연속적인 분포를 갖는데, 이것이 바로 물체에 의해 방출되는 복사의 연속 스펙트럼이라 생각되었다.
흑체 복사 | Blackbody Radiation
흑체 복사란, 흑체라고 간주되는 물체의 공동(空洞, cavity)에서 나온 복사 또는 그 파장분포로 [그림 3]과 같은 그래프 양상을 따른다.
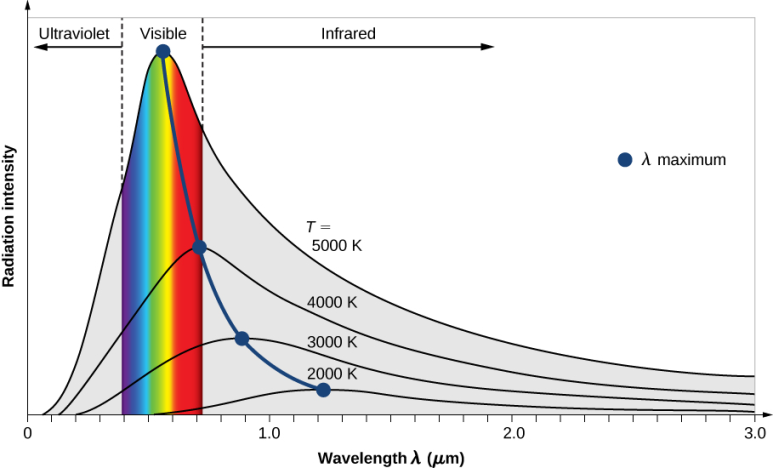
위 그림은 네 개의 온도에 대한 파장에 따른 흑체 복사의 세기 분포로, 여기서 흑체 복사는 5000K의 온도에서 봉우리는 가시광선 영역에 들어와 우리 눈에 보이게 된다.
흑체 복사에 대한 중요한 실험적 발견을 알아보자.
흑체 복사의 중요한 실험적 발견
Key Experimental Discoveries related to Blackbody Radiation
흑체 복사와 관련된 두 가지 실험적 발견을 알아보자.
- 슈테판의 법칙(Stefan's law)
- 빈의 변위법칙(Wien's displacement law)
<<슈테판의 법칙>>

슈테판의 법칙이란, 방출된 복사의 전체 일률은 온도에 따라 급속도로 증가함을 정리한 식이다. 오스트리아의 물리학자 슈테판(Josef Stefan, 1835-1893)이 추론한 식이고, 일률이므로 단위는 와트이다.
슈테판의 법칙
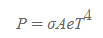
■
<의미>
- P: 물체의 표면에서 방출된 일률, 단위는 와트
- σ: 슈테판-볼츠만 상수
- A: 물체의 표면적, 단위는 제곱미터
- e: 표면의 방출률로 흑체는 e=1이다.
- T: 표면(절대)온도
슈테판의 법칙은 흑체의 단위 면적당 복사에너지가 절대 온도의 네제곱에 비례함을 뜻한다.
<<빈의 변위법칙>>

독일의 물리학자 빌헬름 빈(Wilhelm Wein, 1864-1928)이 1893년 보고한 내용으로, [그림 3]과 같은 파동분포의 봉우리가 온도가 증가함에 따라 더 파장으로 이동함을 아래와 같은 공식으로 나타냈다.
빈의 변위법칙
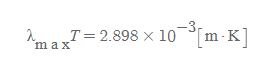
■
<의미>
- λ_max: 복사의 세기분포에서 곡선의 값이 최대가 되는 봉우리의 파장값
- T: 복사를 방출하는 표면의 절대온도
빈의 변위법칙은 흑체 스펙트럼의 봉우리가 온도(가) 증가에 따라 점점 짧은 파장(높은 진동수) 쪽으로 이동함을 정량적으로 잘 설명한다.
흑체복사의 세기분포 해석
Analysis of the Intensity of Blackbody Radiation
흑체로부터 방출되는 에너지 분포를 표현하기 위해 물리량 I(λ, T)를 도입한다. I(λ, T)란, 파장과 온도에 의존하는 흑체 복사에서 방출되는 에너지 세기로 단위 넓이 당 일률로 정의된다.
레일리-진스 법칙

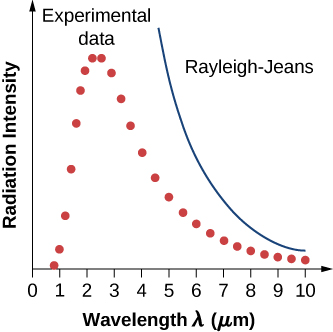
잉글랜드의 물리학자 레일리 남작(John William S. Rayleigh, 1842-1919)과 제임스 진(James Jeans, 1877-1946, 잉글랜드)이 고전물리학에 기초하여 특정한 온도에 있는 흑체의 전자기파 복사의 파장별 세기를 파장에 따라 [그림 4]와 같이 그렸다.
- 흑체 복사의 세기를 고전 전자기학적으로 해석하여 그래프로 나타냈다.
- 전제: 흑체의 공동 벽에서 가속된 전하들에 의해 생긴 전자기장의 많은 진동모드는 모든 파장의 전자기파가 방출되도록 함
- 가정: 정상파의 각 파장에 대한 평균에너지는 에너지 등분배 정리에 근거함
레일리-진스 법칙

■
<의미>
- (k_B)T: 볼츠만 상수에 절대온도를 곱한 값으로 에너지 등분배 정리에 근거한 평균에너지 값이다.
- λ: 복사세기 분포에서의 특정 파장
레일리-진스 법칙에 따르면 파장 λ가 0에 접근할수록 주어진 함수 I(λ, T)는 무한대가 된다. 하지만 [그림 4]의 실제 실험 데이터는 파장 λ가 0에 접근할 수록 I(λ, T)도 0에 근접한다. 이를 자외선 파탄(ultraviolet catastrophe)이라 한다.
파장이 짧을수록 실험 결과 값과 전혀 일치하지 않았으므로, 파장이 짧은 영역에서는 I(λ, T) 값이 지수함수적으로 감소함을 예측하는 수정된 식이 필요했다.
플랑크의 파장분포함수
1900년, 막스 플랑크는 자외선 파탄을 극복하는 새로운 식을 고안했다.
플랑크의 파장분포함수
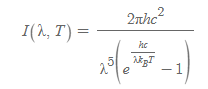
■
<의미>
- h: 플랑크 상수
- c: 진공 조건에서 빛의 속력
플랑크는 파장분포함수를 유도하기 위해 독자적인 모형을 개발했다.
- 흑체복사는 흑체를 구성하는 분자 내 전하를 띤 입자와 연관된 진동자에 의한 것이다. 시스템을 이루는 구성 요소는 전하를 띤 입자진동자로 흑체복사는 이들이 방출한 복사이다.
- 관찰할 수 있는 흑체복사를 방출하는 진동자는 흑체의 표면에 위치한다. 진동자의 에너지는 또한 양자화 되어 있고, 이는 플랑크 상수 h를 포함한 불연속적인 에너지양으로 표현된다.
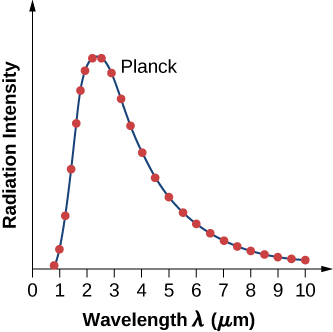
플랑크 모형을 통해 새로운 파장분포함수를 유도했고, 이를 활용해 [그림 5]와 같이 실제 데이터와 일치하는 그래프 결과를 얻었다.
'고급물리학 > 양자역학' 카테고리의 다른 글
| 【물리학 - 양자역학】 03. 광전효과 (2) | 2025.07.23 |
|---|---|
| 【물리학 - 양자역학】 01. 양자역학이란 무엇인가 (0) | 2025.07.19 |
| [물리학-현대물리학] 23. 드브로이 물질파 | Matter Wave(de Broglie Wave) (0) | 2023.12.29 |
| [물리학-현대물리학] 이온결합 | Ionic Bonding (0) | 2023.11.02 |
| 【현대물리학】 복소수 (0) | 2021.12.01 |





