

Erwin Rudolf Josef A. Schrödinger (1887-1961)
오스트리아-헝가리 제국(Österreich-Ungarn Monarchie) 빈에서 출생한 에르빈 슈뢰딩거(Erwin Rudolf Josef A. Schrödinger, 1887-1961)는 전자를 핵 주위의 일정한 궤도를 도는 입자라 생각하는 대신, 파동(파동성을 강조한 입자)으로 모델링했다.
- 전자는 파동함수로 표현된다.
- 파동함수는 일정한 에너지 값을 가지고 있고, 3차원의 공간에서 전자의 위치에 대한 정보를 포함한다.

그림 1. 파동함수는 아래의 그래프처럼 1차원적으로 표현될 수 있고, y축을 기준으로 3차원으로 회전시키면 3차원 공간의 입체상(전자의 위치 정보)을 얻을 수 있다.
보어의 원자 모형에 따르면 전자는 원자핵의 주위에 정해진 궤도를 원운동하므로 정해진 궤도 내에서만 발견되어야 한다. 그러나 (1)전자의 정해진 궤도는 존재하지 않으며, (2)하이젠베르그의 불확정성 원리와 함께 (3)파동방정식을 만족하는 파동함수로 표현될 수 있다.
- 오비탈(orbital): 파동방정식을 만족하는 전자의 파동함수로 원자핵 주위에서 파동과 같이 거동하는 전자를 묘사한다.
- 원자오비탈이란, 원자핵 주위의 공간에서 전자를 발견할 수 있는 확률을 계산할 수 있게 하는 파동함수를 의미한다. 전자의 유의미한 발견확률로 90%이상으로 잡는다.
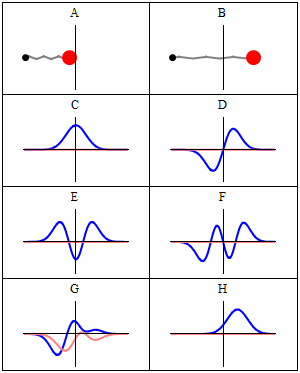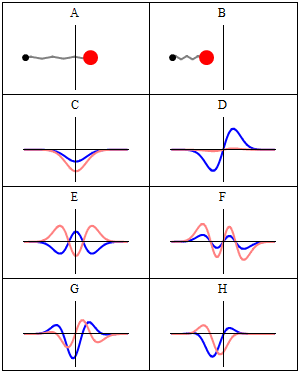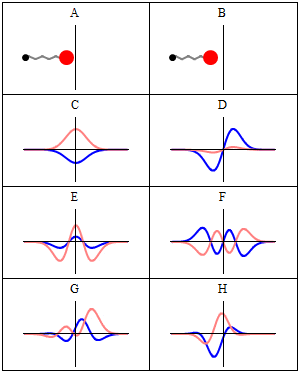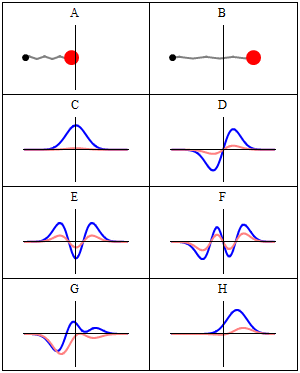
그림 2. Comparison of classical and quantum harmonic oscillator conceptions for a single spinless particle
슈뢰딩거의 파동방정식(1926)
에르빈 슈뢰딩거가 1926년에 고안한 파동역학의 기본 방정식으로 물질파의 개념에 기초를 두고 있으며, 입자의 존재를 '양적으로 기술할 수 있는 존재확률'로 나타낸다.
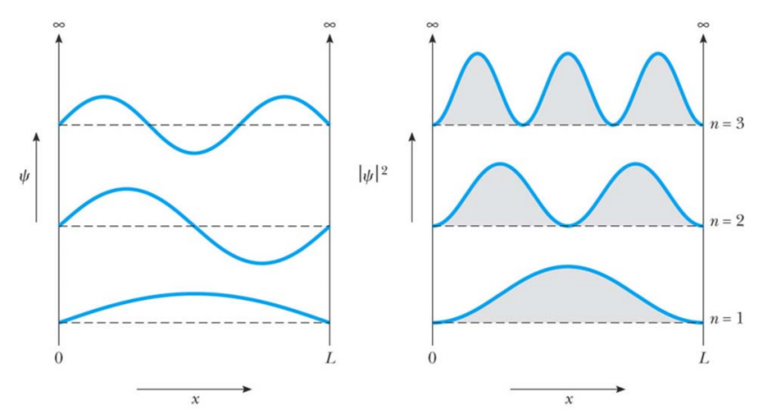
그림 3. 파동함수와 확률밀도(확률분포)

따라서, 어떤 미시공간 ΔV상에 입자가 발견될 확률은 다음과 같이 적을 수 있다.
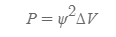

슈뢰딩거 파동방정식
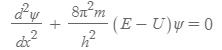
- ψ: 전자(물질파로 표현되는 물질)의 파동함수
- m: 물질파로 표현되는 물질의 질량
- E: 입자의 역학적 에너지
- U: 공간의 퍼텐셜에너지
■
상자 속의 입자: 슈뢰딩거 방정식의 적용

그림 4. 1차원 상자 속의 입자
질량이 m인 입자가 폭이 L인 1차원 상자 내에 왕복운동을 한다고 하자.
- 상자 안의 퍼텐셜에너지(U)는 0이기 때문에 질량체는 자유롭게 움직일 수 있다.
- 상자의 벽은 U가 너무 커 입자가 벽을 뚫지 못한다.
입자의 움직임을 통해 1차원 상자의 퍼텐셜에너지 지도를 다음과 같이 그릴 수 있다.
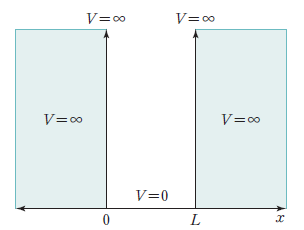
그림 5. 1차원 상자의 퍼텐셜에너지
상자 속의 입자는 상자 외부에 존재할 수 없기 때문에, 상자외부의 퍼텐셜 에너지 U는 무한대로 놓았다.
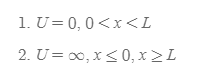
마찬가지로 입자가 상자 외부에 존재할 수 없기 때문에 상자 밖에서는 파동함수가 0으로 관측되어야 한다.
상자 내 입자의 슈뢰딩거 파동방정식
- 상자 내부의 퍼텐셜에너지가 0이므로, 입자의 슈뢰딩거 파동방정식에서 U=0, 역학적 에너지는 운동에너지만 갖는 파동함수 값을 갖는다.

주어진 파동방정식은 상자 내부의 입자의 슈뢰딩거 식으로 입자의 해(solution of wave function)는 다음과 같이 구할 수 있다.
1. 상자의 경계면이 단단한 벽이기 때문에, x=0, x=L에서 파동함수는 0이다.
2. 상자 밖에서 입자가 존재할 확률밀도는 0이고 경계에서도 0이다. 이는 파동에서 고정단 진동의 정상파와 유사하며, 이 조건을 만족시키는 파동의 해는 다음과 같다.
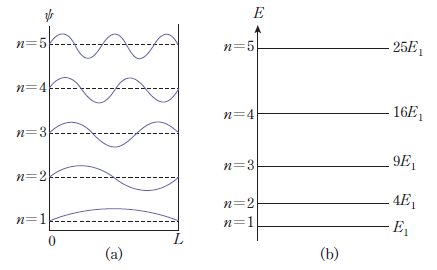
그림 6. 파동함수와 에너지 준위
상자 내부 입자의 슈뢰딩거 방정식의 해
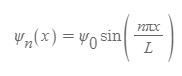
- 슈뢰딩거 방정식의 해에서 n은 에너지 준위에서의 주양자수와 같다.
- n이 무한히 커지면 고전 물리학에서의 입자 발견 확률과 그 의미가 같아 진다.
■
1차원 상자 속 입자의 물질파 특징

그림 7. 1차원 상자 속 입자의 물질파
1. 길이가 L인 1차원의 상자 속에서 움직이는 입자의 파장은 다음 식을 따른다.

주양자수 n이 1일 때 물질파는 '반'파장을 이룬다. 따라서 n=1 조건에서 물질파의 한 파장은 2L만큼의 길이가 필요하다. 다시 말해, n=2일 때, L의 길이에서 물질파는 한 파장을 완벽히 이룬다.
2. 상자 속의 입자의 운동량은 물질파의 정의에 따라, p=h/λ을 따른다.
3. 상자 속 입자가 가질 수 있는 속력은 다음과 같다.

4. 질량 m인 상자 속 입자가 가질 수 있는 운동에너지는 다음과 같이 구해진다.

#화학 #일반화학 #슈뢰딩거 #슈뢰딩거방정식 #파동방정식 #확률밀도 #확률밀도함수 #파동함수 #1차원상자 #상자속입자 #물질파
'대학화학' 카테고리의 다른 글
| [일반화학] 09. 오비탈과 노드(매듭면) (0) | 2020.02.29 |
|---|---|
| [일반화학] 08. 네 가지 양자수 (0) | 2020.02.29 |
| [일반화학] 06. 하이젠베르크의 불확정성 원리 (0) | 2020.02.28 |
| [일반화학] 05. 일전자계의 해석: 보어의 수소원자모형 (0) | 2020.02.28 |
| [일반화학] 04. 수소원자의 선 스펙트럼 (0) | 2020.02.28 |