
중력과 탄성력은 conservative force에 속하며 이들의 PE는 '위치의 함수'로 주어졌다. 힘과 변위로부터 일을 구해 퍼텐셜에너지를 정의했듯이, 위치함수로 주어진 PE로부터 힘을 구할 수 있다.
퍼텐셜에너지로부터 힘 구하기
[1] 미소변위에 대한 힘 F_x의 일은 F_xΔx로 계산할 수 있고, 보존력이 한 일은 위치에너지의 변화량의 (-)의 값이다.
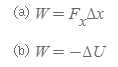
- 식 (b)는 Relationship between Work and Difference of Potential Energy(퍼텐셜에너지의 변화량)와 같다.
[2] 과정 [1]의 식 (a)를 F에 대해 풀 수 있다.
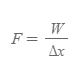
[3] 과정 [2]의 W는 [1]의 식 (b)와 같다.
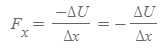
[4] Δx→0이면, F_x의 변화는 무시할 수 있다.

Conservative Force in One Dimension
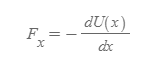
- 1차원 상의 퍼텐셜 에너지의 변화량으로 1차원의 보존력을 구할 수 있다.
■
Conservative Force의 일반식에서 나타나는 특징은 다음과 같다.
1. F_x가 x축의 양의 방향으로 작용하면, x의 증가에 따라 U(x)는 감소(해야) 한다.
2. F_x와 dU/dx는 서로 반대 부호를 갖는다.
3. 보존력이 system에 작용할 경우, 계의 가장(혹은 상대적으로) 낮은 퍼텐셜에너지를 향하도록 작용한다.
Gravitational Force
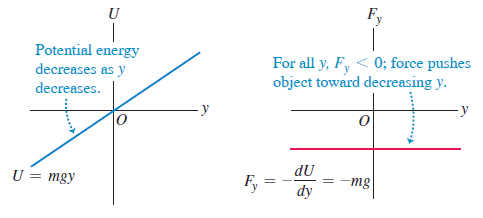
그림 1. y의 함수로 나타낸 중력 퍼텐셜에너지와 중력
중력 PE, mgy를 이용해 g가 일정한 gravitational force를 구할 수 있다.
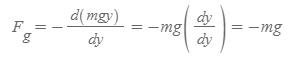
Elastic Force by a Spring
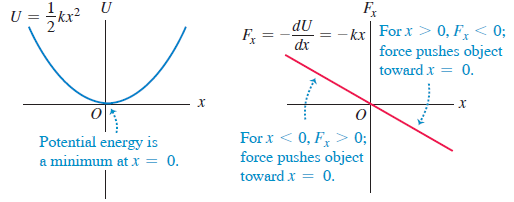
그림 2. x의 함수로 나타낸 탄성 퍼텐셜에너지와 탄성력
탄성력 PE, (kx^2)/2를 이용해 elastic force를 구할 수 있다.
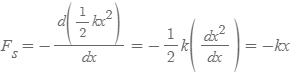
위의 결과는 이상적인 용수철이 가한 힘에 관한 정확한 표현이다.
3차원 상의 보존력
현실 세계의 다수의 실제 입자는 공간에서 x, y, z축으로 자유롭게 움직일 수 있다. 따라서 입자의 PE 함수 U 역시 3차원 상을 고려한 U(x, y, z)라 할 수 있다.
앞선 F_x 식은 x축 성분에 한정된다. 만약 y축과 z축으로 차원을 확장시킨다면, 보존력은 각 axis에 대해 다음과 같이 정리할 수 있다.

입자의 U(x, y, z)는 세 좌표의 함수이므로 식 dU(x, y, z)/dx를 계산한다면,
(1) x 성분은 변수로
(2) y, z 성분은 상수로 간주하여
값을 구한다.
편도함수(partial derivative)의 개념을 이용해 퍼텐셜에너지에서 보존력을 유도할 수 있다.
Conservative Force in Three Dimension
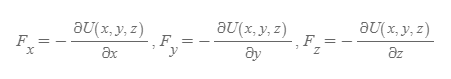
■
힘 F를 단위벡터를 이용해 표현할 수도 있다. ⇒ U의 기울기(gradient)
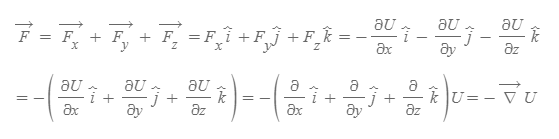
- 델(del)
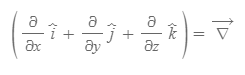
- 3차원 상의 보존력
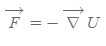
'고급물리학 > 고전역학' 카테고리의 다른 글
| [Mechanics] 초기 역학의 역사 | A Brief History of Early Mechanics (0) | 2020.05.04 |
|---|---|
| [Mechanics] 블랙홀과 슈바르츠실트 반지름 | Black Hole and Schwarzschild Radius (0) | 2020.05.04 |
| [Mechanics] 에너지 보존법칙 | Law of Conservation of Energy (0) | 2020.05.02 |
| [Mechanics] 탄성력과 탄성 퍼텐셜에너지 | Elastic Force and Elastic Potential Energy (0) | 2020.05.02 |
| [Mechanics] 보존력과 비보존력 | Conservative and Nonconservative Forces (0) | 2020.05.01 |