Herald-Lab
미분방정식의 기본개념 본문
미분방정식(differential equation, DE): 미지 함수의 도함수를 포함한 방정식
- 미지의 함수 y=f(x)와 그 도함수 간의 관계를 나타내는 방정식
- 미분방정식의 세 가지 목표
① 특정한 상황을 표현하는 미분방정식의 발견
② 이 미분방정식의 정확한 해를 찾음
③ 찾은 해를 해석하여 미래를 예측함
- 물리학과 공학에서 미분방정식은 동적인 시스템(dynamic system)을 모델링하는 데 일반적으로 활용된다. e.g. 전자와 정공(hole)의 밀도가 시간에 따라 변화하는 반도체 소자
- 미분방정식의 풀이
가령, 아래와 같은 DE가 있다고 하면,
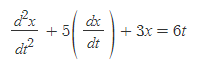
여기서 미분방정식의 풀이란, x(t)를 구하는 것이다.
· 미분방정식의 풀이란, 미분방정식을 만족하는 미지함수, 독립변수의 연속함수인 해를 구하는 것이다.
· 일반적인 대수방정식과는 달리 근은 숫자가 아닌 함수의 형태를 띤다. ⇒ 미분방정식 해(해 함수): 미분방정식에 대입하였을 때 항등적으로 만족시키는 함수
· 미분방정식 해는 기본함수의 항으로 표현가능한 해석적(analytical) 해와 근사값인 수치해석적(numerical method) 해로 나눌 수 있다.
미분방정식의 짧은 역사
- 1671, Newton의 저서인 『Methodus Fluxionum et Serierum Infinitarum』에서, 미분방정식의 해법을 최초로 다룸
· 단, 무한급수를 사용한 계산으로 현대의 미분방정식 풀이와는 거리가 있음
- 신성로마제국 출신의 독일의 철학자 Leibniz(1646-1716)는 라틴어로 미분방정식을 'aequatio differentials'이라고 표현했고, 자신의 적분법으로 미분방정식을 (비교적) 현대적으로 풀어냄

Gottfried Wilhelm von Leibniz, 1646-1716
- 1707, 이탈리아의 수학자 가브리엘레 만프레디(Gabriele Manfredi, 1681-1761)가 최초로 미분방정식의 해법을 다룬 책 『De Constructione Aequationum Differentialium Primi Gradus』를 발간함

Gabriele Manfredi, 1681-1761
· Leibniz의 적분풀이법과 함께 스위스의 수학자 형제 야곱 베르누이(Jacob Bernoulli, 1655-1705)와 요한 베르누이(Johann Bernoulli, 1667-1748)의 풀이법도 함께 수록함
Gabriele persisted with mathematics, studying the works of Leibniz and of Johann and Jacob Bernoulli
on infinitesimal calculus.
- 1739, 스위스의 위대한 수학자 Leonhard P. Euler(1707-1783)는 이후 미분방정식 풀이를 위해 배우게 될 적분인자(integrating factor)를 최초로 고안하기도 함

Jean le Rond d'Alembert, 1717-1783
- 1746, 프랑스 계몽주의 시대의 저명한 수학자 달랑베르(Jean le Rond d'Alembert, 1717-1783)는 1차원 파동방정식을 발견했고, 이후 1747년, 자신의 저서 『기류의 일반적 원인에 대한 고찰(Réflexions sur la cause générale des vents)』에서는 편미분방정식의 풀이법을 또한 제시했다.

미분방정식의 개념
앞선 미분방정식을 통해 몇 가지 개념을 확인해보자.
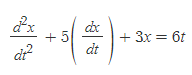
- t: 독립변수
- x: 종속변수 ⇒ 미분이 되는 변수
- d^2x/dt^2, dx/dt: 미지함수의 도함수
미분방정식의 일반적인 형태는 다음과 같이 적을 수 있다.
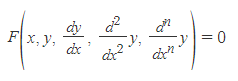
- n: 차수(order) ⇒ 미분방정식의 도함수 중 가장 높은 도함수의 숫자 ⇒ 앞선 예의 order는 2차이다.
선형성 Linearity
- 선형(linearity, linear system)이란, 대단히 복잡한 실제 세계(real world)를 매우 단순하면서 수학적으로 해석가능한 형태로 변환시킨 한 가지 결과물로 '해석 및 설계'를 용이하게 하고자 함에 의미가 있다.
real world의 linearity 또는 linear system은 다음과 같은 특징을 지닌다.
① 대수적 방정식이 선형방정식의 형태를 갖춤

② 기하학적 형태가 직선을 이룸
- 직선 형태의 비례 관계를 만족한다.
③ 중첩의 원리(비례성과 가산성)를 따름
미분방정식의 선형적 특성
① 종속변수와 도함수의 차수가 1차일 때 선형의 특성을 갖는다.
② 종속변수와 도함수의 곱과 연관된 항이 없을 때 선형의 특성을 갖는다. ⇒ y(dy/dx)처럼 종속변수의 곱으로 나타난 항이 있으면 비선형 미분방정식이다.
③ sine 또는 exponential과 같은 종속변수의 비선형 함수가 포함되지 않을 때 선형의 특성을 갖는다. ⇒ y^2, siny, e^y 등과 같은 항이 있으면 비선형 미분방정식이다.
미분방정식의 선형성 판단의 이유는, 이들 유형에 따라 해를 구하는 방법이 매우 달라지기 때문이다.
- 일반적으로, linear DE의 풀이가 non-linear보다 훨씬 간단하다.
EXAMPLE 1.
다음 방정식의 선형, 비선형성을 구분하시오.
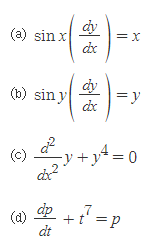
SOLUTION.
(a) 선형
(b) 비선형: siny(dy/dx)
(c) 비선형: y^4
(d) 선형: 종속변수와 도함수의 차수가 일차임
□
해 Solution
미분방정식의 해(solution)는 종속변수와 독립변수의 관계로 해는 지정한 범위 내의 모든 독립변수의 값에 미분방정식이 만족하게 된다.
- 일반해(general soln.): 미분방정식을 만족하는 모든 해
· 어떤 하나의 미분방정식을 만족하는 많은 다른 종류의 해들을 통칭한다.
· 일반해는 적분상수(arbitary constant)를 포함한다. ⇒ 적분상수의 풀이를 위해 조건(condition)이 필요하다.
- 특수해(particular soln.): 주어진 미분방정식을 만족시키는 개별적인 해
· 적분상수의 풀이를 위한 condition을 적용한 특별한 일반해
· 미분방정식에 조건들을 적용하면 particular soln.을 구할 수 있는데, 독립 조건의 개수와 미지수 개수가 서로 같아야 한다.
- 특이해(singular soln.): 일반해로부터 얻어질 수 없는 특이한 해, 일반해에 어떠한 임의 상수를 지정하여도 얻을 수 없는 해 ⇒ 일반해로는 표현이 불가능
해의 표현형태에 따라서는,
① 양함수 해(explicit solution): y=f(x)의 꼴을 갖는 해
② 음함수 해(implicit solution): f(x, y)=0의 꼴을 갖는 해
③ 매개변수 해 형태: x=x(α), y=y(α)의 꼴을 갖는 해
로 분류가 가능하다.
'Calculus > Advanced Calculus' 카테고리의 다른 글
| 단순방정식과 변수분리방정식 (0) | 2021.11.07 |
|---|---|
| 적분표(Table of Integrals) (0) | 2019.09.08 |
| 미분표(Table of Derivatives) (0) | 2019.09.08 |
| 고차 미분: 2차 도함수 (0) | 2019.09.07 |
| 무한소의 활용(Use of Infinitesimals) (0) | 2019.09.07 |




