Herald-Lab
무한소의 활용(Use of Infinitesimals) 본문
x→a일 때,
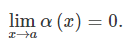
식 1의 함수 α(x)를 무한소(infinitesimal)라고 부른다.
x→a의 조건에서 α(x)와 β(x)를 무한히 작은 크기의 함수라고 할 때, 다음 4가지 극한의 특성을 알아보자.
1.
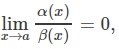
then we can say that the function α(x) is an infinitesimal of higher order than β(x).
2.
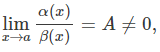
then, the function α(x) and β(x) are called the infinitesimals of the same order.
3.
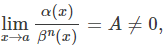
then, the function α(x) is called an infinitesimal of order n compared with the function β(x).
4.
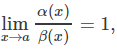
then, the function α(x) and β(x) are said to be equivalent as x→a.
특히 두 개의 무한소 비(ratio of two infinitesimals as x→0 or a)의 극한을 계산할 때, 아래의 표는 극한의 계산을 더 쉽게 만들어 준다.

EXAMPLE 1.
다음 식을 구하시오.
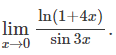
SOLUTION.
표 1에 근거해, ln(1+4x)는 4x로 sin3x는 3x로 근사시킬 수 있다.
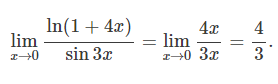
■
EXAMPLE 2.
다음 식을 구하시오.
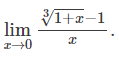
SOLUTION.
3√1+x는 (1+x)^1/3으로 고쳐 쓸 수 있고, 표 1에 근거해 1+x/3으로 근사시킬 수 있다.
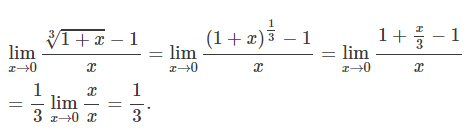
■
EXAMPLE 3.
다음 식을 구하시오.
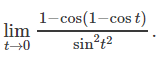
SOLUTION.
- 1-cosx는 x^2/2로 근사할 수 있다.
- sinx는 x로 근사할 수 있다.
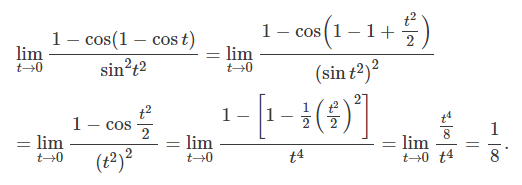
■
'Calculus > Advanced Calculus' 카테고리의 다른 글
| 적분표(Table of Integrals) (0) | 2019.09.08 |
|---|---|
| 미분표(Table of Derivatives) (0) | 2019.09.08 |
| 고차 미분: 2차 도함수 (0) | 2019.09.07 |
| 극한의 부정형의 또 다른 형태와 차수대조법 (0) | 2019.09.06 |
| 엡실론-델타 논법 (0) | 2019.08.30 |




